Cho tam giác ABC nhọn có AB<AC. Có đường phân giác AD. Trên AC lấy E sao cho AE=AB. Vẽ DH⊥AC tại H. BE cắt AD và DH lần lượt tại I và K.Cmr: AK⊥DE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

6 tháng 10 2021
b: Xét ΔAKB vuông tại K và ΔAKC vuông tại K có
AB=AC
AK chung
Do đó: ΔAKB=ΔAKC
Suy ra: KB=KC
Xét ΔMBK vuông tại M và ΔNCK vuông tại N có
KB=KC
\(\widehat{B}=\widehat{C}\)
Do đó: ΔMBK=ΔNCK
Suy ra: KM=KN(1)
Xét ΔAKB vuông tại K có KM là đường cao ứng với cạnh huyền AB
nên \(AM\cdot MB=KM^2\left(2\right)\)
Xét ΔAKC vuông tại K có KN là đường cao ứng với cạnh huyền AC
nên \(AN\cdot NC=KN^2\left(3\right)\)
Từ (1), (2) và (3) suy ra \(AM\cdot MB=AN\cdot NC\)
HN
0



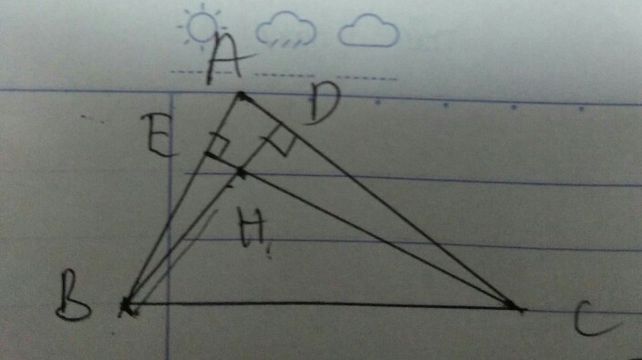
Xét tam giác BAE: AB=AE => Tam giác BAE cân đỉnh A
Ta có: AI là phân giác ^BAE nên AI vuông góc BE hay AD vuông góc EI
Xét tam giác ADE: DH vuông góc AE ; EI vuông góc AD
Mà DH cắt EI tại K => K là trực tâm của tam giác ADE
=> AK vuông góc DE (đpcm).
Xét tam giác ABI và AEI có
AB=AE(gt)
góc BAI=góc IAE( AD phân giác)
AI cạnh chung
=>tam giác ABI=AEI( C-G-C)
=> góc BIA= góc EIA (2 góc tương ứng)
mà BIA+EIA=180 độ
=>BIA=CIA=180 độ/2=90 độ
nên AK vuông góc với KE
Xét tam giác AHD có: HAD+ADH=90*
Xét tam giác EHD có: DEH+HDE=90*
=>ADH+HDE=90*
Vậy, AK vuông góc với DE