Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
`a)` Áp dụng định lý pytago ta có :
`AB^2+AC^2=BC^2`
hay `9^2+12^2=BC^2`
`=>BC^2=225`
`=>BC=15(cm)`
`b)` Xét `ΔABC` và `ΔADC` ta có :
`AC` chung
`\hat{BAC}=90^o`
`\hat{DAC}=90^o`
`=>ΔABC=ΔADC` (c.g.c)
a) Áp dụng định lý Py-ta-go cho \(\Delta\)vuông ABC có:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{5^2+12^2}=13\left(cm\right)\)
b) Xét \(\Delta ABC\)và \(\Delta ADC\)có:
\(\hept{\begin{cases}AB=AD\left(gt\right)\\gócBAC=gócDAC\left(=90^0\right)\\AC:chung\end{cases}}\)
\(\Rightarrow\Delta ABC=\Delta ADC\left(c.g.c\right)-\left(đpcm\right)\)
c) Xét \(\Delta BDC\)có: \(\hept{\begin{cases}\text{A là trung điểm BD}\\AE//BC\left(gt\right)\end{cases}}\)
\(\Rightarrow\text{E là trung điểm CD}\left(t/c\right)\)
Xét \(\Delta ADC\)vuông tại A có AE là đường trung tuyến ứng cạnh DC
\(\Rightarrow AE=\frac{1}{2}CD\left(t/c\right)=EC\left(\text{E là trung điểm CD}\right)\)
\(\Rightarrow\Delta AEC\)cân tại E (đpcm)
d) Gọi giao của AC và BE là O
Xét \(\Delta DBC\)có:\(\hept{\begin{cases}\text{BE là đường trung tuyến ứng cạnh CD }\left(gt\right)\\\text{CA là đường trung tuyến ứng cạnh BD }\left(gt\right)\end{cases}}\)
\(\Rightarrow\)O là trọng tâm của \(\Delta DBC\)
Mà DF là đường trung tuyến ứng cạnh BC
\(\Rightarrow\)CA, DF, BE cùng đồng quy tại 1 điểm (đpcm)
a: \(AC=\sqrt{BC^2-AB^2}=8\left(cm\right)\)
b: Xét ΔABC vuông tại A và ΔADC vuông tại A có
AB=AD
AC chung
Do đó: ΔABC=ΔADC
Á dụng định lý yTaGo vào tam giác vuông ABC ta có
BC2=AC2+AB2
BC2=122+52
BC2=169
Ý b
Xét tam giác ABC và tam giác ADC
góc CAB= góc CAD
AC chung
AB=AD
Vậy tam giác ABC= tam giác ADC(c.g.c)
ý c
Vì tam giác ABC= tam giác ADC(cmt)
suy ra góc ACD= góc ACB
mà AE song song với BC
suy ra góc EAC= góc ACB(hai góc sole trong)
mà góc ACD= góc ACB
vậy tam giác RAC cân tại E
ý d
gọi gia điểm của DF,CA,BE là I
Có FB=FC(F là trung điểm của BC)
AB=AD (gt)
suy ra DF và AC là hai đường trung tuyến của tam giác BDC
mà hai đường này cắt nhau tại I
suy ra I là trọng tâm của tam giác BDC
suy ra BE là đường trung tuyến còn lại
Vậy DF,CA,BE đồng quy tại 1 điểm
Mk thấy đề sai hay sao ý ko có đường thẳng nào đi qua B song song vs CD và cắt DM cả
mik thấy cô ghi đè s mik ghi lại y chang chứ mik ko bik j cả. mik đọc cx thấy sai sai cái j á mà ko bik mik đọc đè đúng hay là sai nên mik mới đăng
xét tam giác abc vuông tại a có
a) bc2=ac2+ab2=122+52=132
bc=13
b)xét tam giác abc vá tam giac adc có
ab=ad
góc bac= góc dac
ac là cạnh chung
=>tam giác abc =tam giác adc (c.g.c)
c)
Cho tam giác ABC vuông tại A với AB = 3cm, BC= 5cm
a) tính độ dài đoạn thẳng AC
b) trên tia đối của tia AB, lấy điểm D sao cho AB = AD. Chứng minh tam giác ABC = tam giác ADC, từ đó suy ra tam giác BCD cân
a/Áp dụng định lí Pytago và tam giác ABC vuông tại A:
BC2=AB2+AC2
=>AC2=BC2-AB2=102-62=100-36=64
=> AC=\(\sqrt{64}=8cm\)
b/ Xét tam giác ABC và tam giác ADC có:
AC chung
góc BAC=DAC=90 độ
AD=AB(gt)
=> Tam giác ABC=tam giác ADC(c-g-c)
a) xét tam giác ABC và tam giác ACD có:
góc A = 900
AB = AD ( gt)
=> tam giác ABC = tam giác ACD
=> BC = CD (cạnh tương ứng)
=> tam giác BCD cân tại C
sai rùi bn !!!!!!!!!!!!!!!!!!!!!
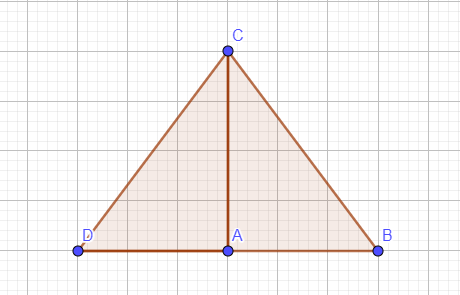
a) Áp dụng định lý Py-ta-go, ta có:
\(BC^2=AB^2+AC^2\)
\(BC^2=5^2+12^2\)
\(\Rightarrow BC^2=169\left(cm\right)\)
\(\Rightarrow BC=\sqrt{169}=13\left(cm\right)\)
b) Vì \(\Delta ABC=\Delta ADC\)
\(\Rightarrow\widehat{C_1}=\widehat{C_2}\left(2\text{ góc tương ứng}\right)\)
Vì BC // AE (gt)
\(\Rightarrow\widehat{CED}=\widehat{C_1}\left(\text{so le}\right)\)
\(\Rightarrow\Delta EAC\text{ là tam giác cân. }\)
=> ĐPCM
d) Ta có: BF = CF (F là trung điểm của BC)
AB = AD (gt)
=> DP và AB là 2 đường trung tuyến của tam giác BDC
=> G là trọng điểm của tam giác BDC
=> BG là đường trung tuyến còn lại của tam giác BDC
<=> CA; DF; BE cùng đi qua 1 điểm hoặc CA; DF; BE đồng quy tại 1 điểm
=> ĐPCM
P/s: Mk vẽ hình hơi xấu, mong bn thông cảm