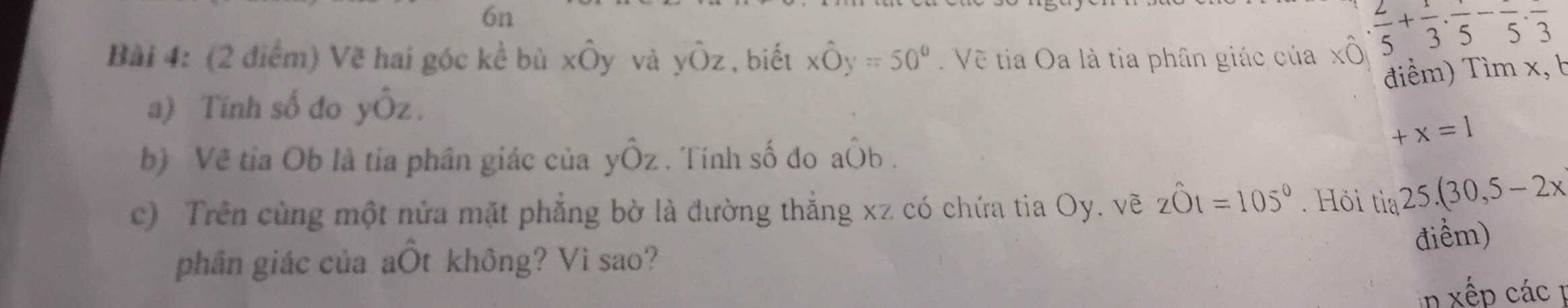Giải chi tiết, ko cần hình
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 6 2021
Hình tự vẽ
Hình thang AB//CD, AB<CD
Từ đỉnh A và B của đáy bé, hạ đường vuông góc AF và BE
Ta được hình vuông ABEF
Ta có AB?//CD
⇒ ∠ BAC + ∠ADC = 180\(^0\) ( hai góc trong cùng phía ) (*)
Lại có ∠BAD = ∠BAF + ∠FAD
⇔ ∠BAD = 90\(^0\) + ∠FAD
⇔ ∠BAD > 90\(^0\)
Từ (*) ⇒ ∠BAD > ∠ADC (1)
Chứng minh tương tự ta được
⇒ ∠ABC > ∠BCD (2)
Từ (1) và (2)
⇒ ∠BAD + ∠ABC > ∠ADC + ∠BCD (dpcm)
Vậy tổng hai góc kề đáy nhỏ lớn hơn tổng hai góc kề đáy lớn
MN
11 tháng 6 2021
Từ B kẽ BE vuông góc với CD :
\(\Rightarrow AB=DE=11\left(cm\right)\)
\(TC:\)
\(BE=AD=12\left(cm\right)\)
Áp dụng định lý Pytago trong tam giác vuông BEC :
\(EC=\sqrt{BC^2-BE^2}=\sqrt{13^2-12^2}=5\left(cm\right)\)
\(KĐ:\)
\(DC=DE+EC=11+5=16\left(cm\right)\)
Áp dụng định lý Pytago trong tam giác vuông ADC :
\(AC=\sqrt{AD^2+DC^2}=\sqrt{12^2+16^2}=20\left(cm\right)\)
NB
2
20 tháng 4 2021
a) vì xoy+yoz=180 độ(2 góc kề bù)
=> yoz=180-xoy=130 độ
20 tháng 4 2021
vì oa là tia phân giác của xoy
=> xoa=aoy=xoy/2=50/2=25độ
vì ob .................................yoz
=> yob=boz=yoz/2=130/2=65độ
=> aob=aoy+yob=25+65=90độ
5 tháng 3 2022
Câu 3:
a: \(BD=\sqrt{BC^2-DC^2}=4\left(cm\right)\)
b: \(\widehat{A}=180^0-2\cdot70^0=40^0< \widehat{B}\)
nên BC<AC=AB
c: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó:ΔEBC=ΔDCB
d: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O
