Cho tam giác ABC vuông tại A có AB = 3cm, AC = 4cm. Điểm I nằm trong tam giác và cách đều ba cạnh của tam giác ABC. Gọi M là chân đường vuông góc kẻ từ điwwmr I đến BC. Tính BM?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 3 2017
Tam giác ABC vuông tại A => BC2 = AB2 + AC2 ( Theo định lý pitago )
=> BC2 = 32 + 42 = 9 + 16 = 25 = 52
=> BC = 5 (cm)
Tam giác IBC có IB = IC => Góc IBM = Góc ICM (định lý)
Xét tam giác BIM và tam giác CIM có :
IB = IC (gt)
Góc IBM = Góc ICM (cm trên)
Góc BMI = Góc IMC = 900 (gt)
=> tam giác BIM = tam giác CIM (CH - GN)
=> BM = MC (góc tương ứng)\
Mà BM + MC = BC = 5(cm)
=> BM + BM = 5 <=> 2BM = 5 => BM = 2,5 (cm)
Vậy BM = 2,5 (cm)
T
14 tháng 7 2019
#)Góp ý :
Bạn tham khảo nhé ^^
Xét tam giác ABC vuông tại A :
BC2 = AB2 + AC2 (định lý Py-ta-go)
=> BC2 = 32 + 42 = 9 + 16 = 25
=> BC = 5 cm
Ta có : IB = IC (I cách đều 3 cạnh của tam giác ABC)
=> Tam giác IBC cân tại I
=> Góc IBM = góc ICM
Xét tam giác BIM và tam giác CIM có :
Góc BMI = góc CMI (= 90 độ)
IB = IC (cmt)
Góc IBM = góc ICM (cmt)
==> Tam giác BIM = tam giác CIM (cạnh huyền - góc nhọn)
=> BM = CM (2 cạnh tương ứng)
mà BM + CM = BC = 5 cm
Nguồn : Câu hỏi của Nguyen Ngoc Anh Linh - Toán lớp 7 | Học trực tuyến
Link : https://h.vn/hoi-dap/question/567650.html
Điểm I nằm trong tam giác và cách đều 3 cạnh tam giác ABC. Gọi M là chân đường vuông góc kẻ từ I đến BC. Tính MB.
CM
30 tháng 5 2017
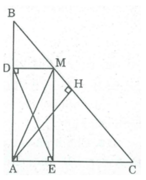
Xét tứ giác ADME, ta có:
∠ A= 90 0 (gt)
MD ⊥ AB (gt)
⇒ ∠ (ADM) = 90 0
Lại có, MD ⊥ AC ⇒ ∠ (MEA) = 90 0
Suy ra tứ giác ADME là hình chữ nhật (vì có 3 góc vuông)
∆ ABC vuông cân tại A ⇒ ∠ B = 45 0 và AB = AC = 4cm
Suy ra: ∆ DBM vuông cân tại D
⇒ DM = DB
Chu vi hình chữ nhật ADME bằng:
2(AD + DM) = 2(AD + DB) = 2AB = 2.4 = 8 (cm)
AH
Akai Haruma
Giáo viên
7 tháng 9 2021
Lời giải:
Ta có:
$AB.AC=AH.BC=40$
$AB^2+AC^2=BC^2=100$
$\Rightarrow (AB+AC)^2=AB^2+AC^2+2AB.AC=180$
$\Rightarrow AB+AC=6\sqrt{5}$
Theo định lý Viet đảo, $AB,AC$ là nghiệm của pt $X^2-6\sqrt{5}X+40=0$
$\Rightarrow AB=4\sqrt{5}; AC=2\sqrt{5}$ (giả sử $AB>AC$)
Dễ thấy $AIHK$ là hình chữ nhật do có 3 góc vuông $\widehat{A}=\widehat{I}=\widehat{K}=90^0$
$\Rightarrow IK=AH=4$
Theo định lý Pitago: $AI^2+AK^2=IK^2=16(1)$
Mặt khác, theo hệ thức lượng trong tam giác vuông:
$AI.AB=AH^2$
$AK.AC=AH^2$
$\Rightarrow AI.AB=AK.AC\Rightarrow \frac{AI}{AK}=\frac{AC}{AB}=\frac{2\sqrt{5}}{4\sqrt{5}}=\frac{1}{2}(2)$
Từ $(1);(2)\Rightarrow AI=\frac{4\sqrt{5}}{5}; AK=\frac{8\sqrt{5}}{5}$ (cm)
Chu vi AIHK:
$P=2(AI+AK)=2(\frac{4\sqrt{5}}{5}+\frac{8\sqrt{5}}{5})=\frac{24\sqrt{5}}{5}$ (cm)
Diện tích AIHK:
$S=AI.AK=\frac{4\sqrt{5}}{5}.\frac{8\sqrt{5}}{5}=6,4$ (cm vuông)
CM
19 tháng 5 2019
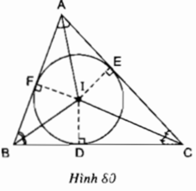
Theo tính chất tia phân giác, ta có:
AI là tia phân giác của góc BAC
⇒ IE = IF
Tương tự: CI là tia phân giác của góc ACB
⇒ IE = ID
Do đó: IE = IF = ID
Vậy 3 điểm D, E, F cùng nằm trên đường tròn tâm I
bạn làm dc chưa