tìm giá trị nhỏ nhất của biểu thức
Q=x2+2y2+4x+6y+1
mọi người giúp mk vs
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HS
1
17 tháng 10 2021
\(A=x^2-4x+9=\left(x-2\right)^2+5\ge5\forall x\)
Dấu '=' xảy ra khi x=2
\(B=x^2-x+1=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)
PT
1
CM
9 tháng 2 2017
Q = x 2 + 2 y 2 + 2 x y − 2 x − 6 y + 2015 = x 2 + 2 x y + y 2 − 2 x − 2 y + 1 + y 2 − 4 y + 4 + 2010 = x 2 + 2 x y + y 2 − 2 x + 2 y + 1 + y 2 − 4 y + 4 + 2010 = x + y 2 − 2 x + y + 1 + y 2 − 4 y + 4 + 2010 = x + y − 1 2 + y − 2 2 + 2010
HT
1
30 tháng 5 2022
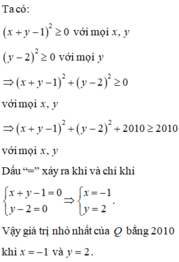
\(A=\left(x^2-2xy+y^2\right)+2\left(x-y\right)+1+y^2-8y+16-17\\ A=\left(x-y+1\right)^2+\left(y-4\right)^2-16\ge17\)
Vậy \(A_{min}=17\leftrightarrow\left\{{}\begin{matrix}x-y+1=0\\y-4=0\end{matrix}\right.\leftrightarrow\left\{{}\begin{matrix}x=3\\y=4\end{matrix}\right.\)
CM
29 tháng 7 2019
A = x 2 + 2 y 2 – 2 x y + 2 x – 10 y ⇔ A = x 2 + y 2 + 1 – 2 x y + 2 x – 2 y + y 2 – 8 y + 16 – 17 ⇔ A = ( x 2 + y 2 + 12 – 2 . x . y + 2 . x . 1 – 2 . y . 1 ) + ( y 2 – 2 . 4 . y + 4 2 ) – 17 ⇔ A = ( x – y + 1 ) 2 + ( y – 4 ) 2 – 17
Vì với mọi x; y nên A ≥ -17 với mọi x; y
=> A = -17
⇔ x − y + 1 = 0 y − 4 = 0 ⇔ x = y − 1 y = 4 ⇔ x = 3 y = 4
Vậy A đạt giá trị nhỏ nhất là A = -17 tại x = 3 y = 4
Đáp án cần chọn là: B
NT
1
S
29 tháng 12 2020
A= x2+2y2-2xy-2x-2y+1015
A = x2 - 2xy - 2x + y2 + 2y + 1 + y2 - 4y + 4 + 1010
A = [x2 - 2x(y + 1) + (y+1)2 ] + (y-2)2 + 1010
A = ( x - y - 1)2 + (y-2)2 + 1010 \(\ge1010\forall x,y\)
Dấu "=" xảy ra <=> \(\left\{{}\begin{matrix}x-y-1=0\\y-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=2\end{matrix}\right.\)
Vậy MinA = 1010 <=> \(\left\{{}\begin{matrix}x=3\\y=2\end{matrix}\right.\)
CM
20 tháng 3 2019
A = x 2 + 2 y 2 – 2 x y + 2 x – 10 y ⇔ A = x 2 + y 2 + 1 – 2 x y + 2 x – 2 y + y 2 – 8 y + 16 – 17 ⇔ A = ( x 2 + y 2 + 1 2 – 2 . x . y + 2 . x . 1 – 2 . y . 1 ) + ( y 2 – 2 . 4 . y + 4 2 ) – 17 ⇔ A = ( x – y + 1 ) 2 + ( y – 4 ) 2 – 17
Vì x - y + 1 2 ≥ 0 y - 4 2 ≥ 0 với mọi x, y nên A ≥ -17 với mọi x, y
=> A = -17 ó x - y + 1 = 0 y - 4 = 0 ó x = y - 1 y = 4 ó x = 3 y = 4
Vậy A đạt giá trị nhỏ nhất là A = -17 tại x = 3 y = 4
Đáp án cần chọn là: C
N
1
13 tháng 1 2022
\(A=\left[\left(x^2-2xy+y^2\right)+2\left(x-y\right)+1\right]+\left(y^2-8y+16\right)-17\\ A=\left(x-y+1\right)^2+\left(y-4\right)^2-17\ge-17\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x-y+1=0\\y-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=y-1=3\\y=4\end{matrix}\right.\)
\(Q=x^2+2y^2+4x+6y+1\)
\(Q=\left(x^2+4x+4\right)+2\left(y^2+3y+\frac{9}{4}\right)-\frac{15}{2}\)
\(Q=\left(x+2\right)^2+2\left(y+\frac{3}{2}\right)^2-\frac{15}{2}\ge-\frac{15}{2}\)
Dấu "=" xảy ra khi: \(\hept{\begin{cases}x=-2\\y=-\frac{3}{2}\end{cases}}\)