Giải phương trình nghiệm nguyên : 4x2 + 4x + y2 - 6y = 24
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu hỏi của Hà thúy anh - Toán lớp 8 | Học trực tuyến Vừa có ng giải xong


a)2x2+4x=19-3y2
⇔2x2+4x+2=21-3y2
⇔2(x+1)2=3(7-y2)Ta có 2(x+1)2⋮2⇒3(7-y2)⋮2
⇒7-y2⋮2
⇒y lẻ (1)
Ta lại có 2(x+1)2≥0
⇒3(7-y2)≥0
⇒7-y2≥0
⇒y2≤7
⇒y2∈{1;4} (2)
Từ (1),(2)⇒y2∈{1}
⇒y∈{-1;1}
Ta có y2=1⇒2(x+1)2=3(7-y2)=18⇒(x+1)2=9
⇒x+1=3 hoặc x+1=-3
⇒x=2 hoặc x=-4
Vậy {x,y}={(-1;2);(-1;-4);(1;2);(1;-4)}

4x2 – 4x + 1 = 0;
a = 4; b = -4; c = 1
Δ = b2 - 4ac = (-4)2 - 4.4.1 = 16 - 16 = 0
⇒ phương trình có nghiệm kép
x = (-b)/2a = (-(-4))/2.4 = 1/2
Vậy phương trình có nghiệm duy nhất x = 1/2

Vì \(4x⋮2;6y⋮2;10⋮2\)nên \(-5z⋮2\Rightarrow z⋮2\)(vì (-5;2)=1)
Đặt \(z=2k\left(k\in Z\right)\)
Khi đó: \(4x+6y-5z=10\Leftrightarrow4x+6y-10k=10\Leftrightarrow2x+3y-5k=5\Leftrightarrow2x=5+5k-3y\)
\(\Leftrightarrow x=\frac{5+5k-3y}{2}\Leftrightarrow x=\frac{4+4k-2y+1+k-y}{2}=2+2k-y+\frac{1+k-y}{2}\)
Đặt \(\frac{1+k-y}{2}=t\left(t\in Z\right)\)
\(\Leftrightarrow1+k-y=2t\Leftrightarrow y=1+k-2t\)
Khi đó \(x=2+2k-y+\frac{1+k-y}{2}=2+2k-1-k+2t+t=1+k+3t\)
Vậy x=1+k+3t: y=1+k-2t với \(k,t\in Z\)

\(A=-\left(4x^2-4x+1\right)-\left(y^2+6y+9\right)+11\\ A=-\left(2x-1\right)^2-\left(y+3\right)^2+11\le11\\ A_{max}=11\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=-3\end{matrix}\right.\)
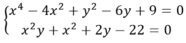
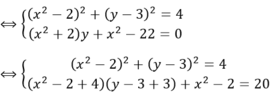


Ak mk bị nhầm tí sorry nha giải tiếp đoạn đó nha
(2x+1)^2+(y-3)^2 = 34 = 5^2 + 9^2
<=> (2x+1)^2 = 5^2 ; (y-3)^2 = 9^2 hoặc (2x+1)^2 = 9^2 ; (y-3)^2 = 5^2
<=> x=2 hoặc x=-3 ; y=12 hoặc y=-6
hoặc :
x=4 ; x=-5 hoặc y=8 ; y=-2
Vậy ............
Tk mk nha
pt <=> (4x^2+4x+1)+(y^2-6y+9) = 14
<=>(2x+1)^2 + (y-3)^2 = 14
<=> (2x+1)^2 = 14 - (y-3)^2 < = 14
Mà 2x+1 lẻ nên (2x+1)^2 thuộc {1;9}
+, Với (2x+1)^2 = 1 => (y-3)^2 = 13 => ko tồn tại y thuộc Z
+, Với (2x+1)^2 = 9 => (y-3)^2 = 5 => ko tồn tại y thuộc Z
Vậy ko tồn tại cặp số x,y thuộc Z t/m pt
Tk mk nha