Tính:a)(1-1/4).(1-1/9).(1-1/16)....(1-1/225)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
8 tháng 11 2016
A=3/4x8/9x15/16x...x224/225
A=3.8.15....224/4.9.16...225
A=(1.3)(2.4)(3.5)...(14.16)/2.2.3.3....15.15
A=(1.2.3...14)(3.4.5...16)/(2.3...15)(2.3...15)
A=16/15.2
A=8/15
PT
0
17 tháng 10 2018
a,\(\left(\frac{1}{9}-1\right).\left(\frac{1}{10}-1\right)...\left(\frac{1}{2004}-1\right).\left(\frac{1}{2005}-1\right)\)
\(=\frac{-8}{9}.\frac{-9}{10}...\frac{-2003}{2004}.\frac{-2004}{2005}\)
\(=\frac{\left(-8\right).\left(-9\right)...\left(-2003\right).\left(-2004\right)}{9.10...2004.2005}\)
\(=\frac{-\left(8.9...2003.2004\right)}{9.10...2004.2005}\)
\(=\frac{-8}{2005}\)
b,Ta có: \(81^{10}-27^{13}-9^{21}\)
\(=\left(3^4\right)^{10}-\left(3^3\right)^{13}-\left(3^2\right)^{21}\)
\(=3^{40}-3^{39}-3^{42}\)
\(=3^{39}.3-3^{39}-3^{39}.3^3\)
\(=3^{39}.\left(3-1-3^3\right)\)
\(=3^2.3^{37}.\left(-25\right)\)
\(=3^{37}.\left(-225\right)⋮225\)
Vậy \(81^{10}-27^{13}-9^{21}⋮225\)
HP
3
5 tháng 8 2021
\(a)\)
\(2^{2x-1}+6.2^8=14.2^8\)
\(\Leftrightarrow2^{2x-1}=14.2^8-6.2^8\)
\(\Leftrightarrow2^{2x-1}=8.2^8\)
\(\Leftrightarrow2^{2x-1}=2^3.2^8\)
\(\Leftrightarrow2x-1=11\)
\(\Leftrightarrow2x=11+1\)
\(\Leftrightarrow x=\frac{12}{2}\)
\(\Leftrightarrow x=6\)
5 tháng 8 2021
\(b)\)
\(A=\left(1-\frac{1}{4}\right)\left(1-\frac{1}{9}\right)\left(1-\frac{1}{16}\right)\left(1-\frac{1}{25}\right)...\left(1-\frac{1}{196}\right)\left(1-\frac{1}{225}\right)\)
\(\Leftrightarrow A=\frac{3}{4}.\frac{8}{9}...\frac{224}{225}\)
\(\Leftrightarrow A=\frac{1.3}{2.2}.\frac{2.4}{3.3}...\frac{14.16}{15.15}\)
\(\Leftrightarrow A=\frac{1.2.3.4...14.16}{2.2.3.3...25.25}\)
\(\Leftrightarrow A=\frac{1.2.3...14}{2.3.4...15}.\frac{3.4.5...16}{2.3.4...15}\)
\(\Leftrightarrow A=\frac{1}{15}.\frac{16}{2}\)
\(\Leftrightarrow A=\frac{8}{15}\)
30 tháng 6 2021
a) Ta có: \(\dfrac{-4}{3}\cdot\sqrt{\left(-0.4\right)^2}\)
\(=-\dfrac{4}{3}\cdot0.4\)
\(=\dfrac{-1.6}{3}=-\dfrac{8}{15}\)
b) Ta có: \(\sqrt[3]{\dfrac{3}{4}}\cdot\sqrt[3]{\dfrac{9}{16}}\)
\(=\sqrt[3]{\dfrac{27}{64}}=\dfrac{3}{4}\)
c) Ta có: \(\dfrac{1}{3+\sqrt{2}}+\dfrac{1}{3-\sqrt{2}}\)
\(=\dfrac{3-\sqrt{2}+3+\sqrt{2}}{7}\)
\(=\dfrac{6}{7}\)
27 tháng 7 2021
a) Ta có: \(\dfrac{-5}{7}\left(\dfrac{14}{5}-\dfrac{7}{10}\right):\left|-\dfrac{2}{3}\right|-\dfrac{3}{4}\left(\dfrac{8}{9}+\dfrac{16}{3}\right)+\dfrac{10}{3}\left(\dfrac{1}{3}+\dfrac{1}{5}\right)\)
\(=\dfrac{-5}{7}\cdot\dfrac{3}{2}\cdot\dfrac{21}{10}-\dfrac{3}{4}\cdot\dfrac{56}{3}+\dfrac{10}{3}\cdot\dfrac{8}{15}\)
\(=\dfrac{-9}{4}-14+\dfrac{16}{9}\)
\(=\dfrac{-1621}{126}\)
b) Ta có: \(\dfrac{17}{-26}\cdot\left(\dfrac{1}{6}-\dfrac{5}{3}\right):\dfrac{17}{13}-\dfrac{20}{3}\left(\dfrac{2}{5}-\dfrac{1}{4}\right)+\dfrac{2}{3}\left(\dfrac{6}{5}-\dfrac{9}{2}\right)\)
\(=\dfrac{-17}{26}\cdot\dfrac{13}{17}\cdot\dfrac{-3}{2}-\dfrac{20}{3}\cdot\dfrac{3}{20}+\dfrac{2}{3}\cdot\dfrac{-33}{10}\)
\(=\dfrac{3}{4}-1-\dfrac{11}{5}\)
\(=-\dfrac{49}{20}\)
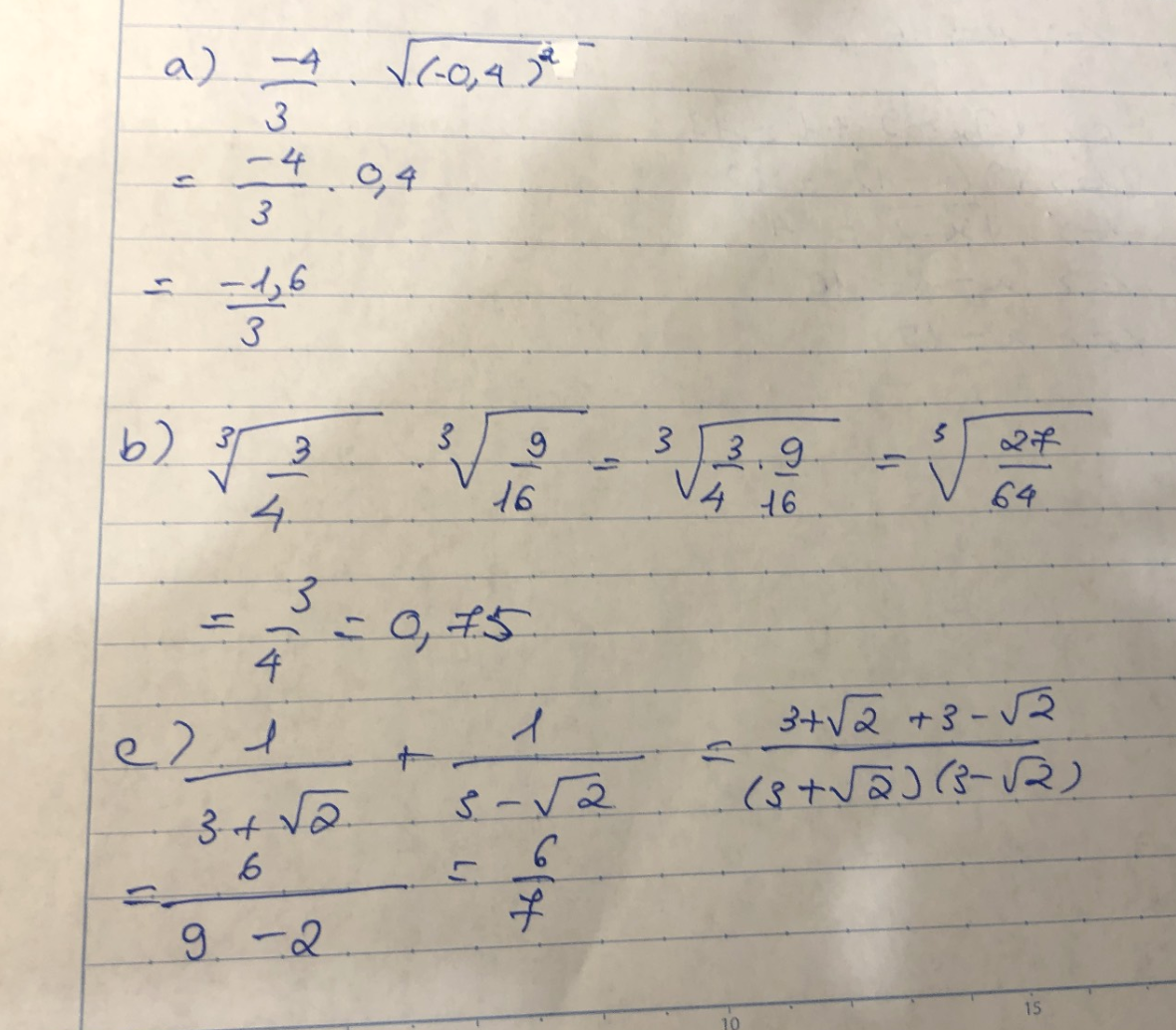
\(\left(1-\frac{1}{4}\right)\left(1-\frac{1}{9}\right)...\left(1-\frac{1}{225}\right)\)
\(=\frac{3}{4}\cdot\frac{8}{9}\cdot...\cdot\frac{224}{225}\)
\(=\frac{1\cdot3}{2\cdot2}\cdot\frac{2\cdot4}{3\cdot3}\cdot...\cdot\frac{14\cdot16}{15\cdot15}\)
\(=\frac{1\cdot3\cdot2\cdot4\cdot...\cdot14\cdot16}{2\cdot2\cdot3\cdot3\cdot...\cdot25\cdot25}\)
\(=\frac{\left(1\cdot2\cdot3\cdot...\cdot14\right)\cdot\left(3\cdot4\cdot5\cdot...\cdot16\right)}{\left(2\cdot3\cdot4\cdot...\cdot15\right)\cdot\left(2\cdot3\cdot4\cdot...\cdot15\right)}\)
\(=\frac{1\cdot2\cdot3\cdot...\cdot14}{2\cdot3\cdot4\cdot...\cdot15}\cdot\frac{3\cdot4\cdot5\cdot...\cdot16}{2\cdot3\cdot4\cdot...\cdot15}\)
\(=\frac{1}{15}\cdot\frac{16}{2}\)
\(=\frac{1}{15}\cdot8\)
\(=\frac{8}{15}\)
( 1- 1/4 ) . ( 1 - 1/9 ) . ( 1 - 1/16 ) ...( 1 - 1/225 )
= 3/4 . 8/9 . 15/16 ... 224/225
= 3 . 8 . 15 ... 224 / 4 . 9 . ..225
= 3 . 2 . 4 . 3 . 5 ... 14 . 16 / 2 . 2 . 3 . 3 ... 15 . 15
= ( 3 . 4 . 5 ... 16 ) . ( 2 . 3 . 4 ... 14 ) / ( 2 . 3 ... 15 ) . ( 2 . 3 ... 15 )
= 16/ 2 . 15
= `8/15