u và v là cá số thực dương thỏa mãn u + v =4
Tìm GTNN của \(P=u^2+v^2+\frac{33}{uv}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
0
T
12 tháng 5 2019
Câu a em nghĩ có thể làm như vầy ạ,câu b để sau (em mới lớp 7,cần suy ra nghĩ thêm)
a)ĐKXĐ: x > 4; \(y\ne2\)
Đặt \(\frac{1}{\sqrt{x-4}}=a;\frac{1}{y+2}=b\)
Hệ phương trình trở thành: \(\hept{\begin{cases}3a+4b=7\\5a-b=4\end{cases}}\Leftrightarrow\hept{\begin{cases}3a+4b=7\\20a-4b=16\end{cases}}\)
Cộng theo vế với vế của hai phương trình trong hệ,ta được: \(23a=7+16=23\Rightarrow a=1\Rightarrow b=1\)
Đến đây dễ rồi ạ.
DT
cho x,y là 2 số dương thỏa mãn x+y=1 , tìm GTNN của A= \(\frac{x}{\sqrt{1-x}}+\frac{y}{\sqrt{1-y}}\)
2
22 tháng 8 2021
Bạn vào link tham khảo :
https://hoidap247.com/cau-hoi/1226651
# Hok tốt !
22 tháng 8 2021
\(x+y=1\Rightarrow\hept{\begin{cases}1-x=y\\1-y=x\end{cases}}\)
thay vào A ta được : \(A=\frac{1-y}{\sqrt{y}}+\frac{1-x}{\sqrt{x}}\)
\(\Rightarrow A=\frac{1}{\sqrt{y}}-\sqrt{y}+\frac{1}{\sqrt{x}}-\sqrt{x}\)
\(\Rightarrow A=\left(\frac{1}{\sqrt{x}}+\frac{1}{\sqrt{y}}\right)-\left(\sqrt{x}+\sqrt{y}\right)\)
áp dụng \(\frac{1}{a}+\frac{1}{b}\ge\frac{4}{a+b}\) ta có : \(\frac{1}{\sqrt{x}}+\frac{1}{\sqrt{y}}\ge\frac{4}{\sqrt{x}+\sqrt{y}}\)
áp dụng \(\left(a+b\right)^2\le2\left(a^2+b^2\right)\) ta có : \(\left(\sqrt{x}+\sqrt{y}\right)^2\le2\left(\sqrt{x}^2+\sqrt{y}^2\right)=2\)
\(\Rightarrow\sqrt{x}+\sqrt{y}\le\sqrt{2}\)
\(\Rightarrow A\ge\sqrt{8}-\sqrt{2}=\sqrt{2}\)
dấu = xảy ra khi a=y=1/2
3 tháng 4 2023
b: Phương trình cần tìm là x^2+8x-105=0
=>(x+15)(x-7)=0
=>x=-15 hoặc x=7
c: Phương trình có hai nghiệm u,v thỏa mãn là x^2-2x+9=0
=>PTVN
d: Phương trình có hai nghiệm u,v thỏa mãn là x^2-5x+24=0
=>PTVN
TN
2
VN
4 tháng 4 2017
Tức là như thế này:
a/ \(u+v=32\Rightarrow u=32-v\)hoặc \(v=32-u\)(Cái này tùy bạn chọn nhưng mình chọn cái 1)
Ta có: \(uv=231\)
\(\Leftrightarrow\left(32-v\right)v=231\)
\(\Leftrightarrow32v-v^2-231=0\)
\(\Leftrightarrow-v^2+32v-231=0\)
Sau đó bạn giải \(\Delta\)tìm được \(v\)và có \(v\)rồi thì ra cái còn lại.
Các câu sau tương tự không có gì hết
CM
18 tháng 7 2017
a) S = 32 ; P = 231 ⇒ S 2 – 4 P = 322 – 4 . 231 = 100 > 0
⇒ Tồn tại u và v là hai nghiệm của phương trình: x 2 – 32 x + 231 = 0 .
Ta có: Δ = ( - 32 ) 2 – 4 . 231 = 100 > 0
⇒ PT có hai nghiệm:
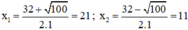
Vậy u = 21 ; v = 11 hoặc u = 11 ; v = 21.
b) S = -8; P = -105 ⇒ S 2 – 4 P = ( - 8 ) 2 – 4 . ( - 105 ) = 484 > 0
⇒ u và v là hai nghiệm của phương trình: x 2 + 8 x – 105 = 0
Ta có: Δ ’ = 4 2 – 1 . ( - 105 ) = 121 > 0
Phương trình có hai nghiệm:
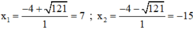
Vậy u = 7 ; v = -15 hoặc u = -15 ; v = 7.
c) S = 2 ; P = 9 ⇒ S 2 – 4 P = 2 2 – 4 . 9 = - 32 < 0
⇒ Không tồn tại u và v thỏa mãn.
29 tháng 5 2017
Ta có: \(\hept{\begin{cases}\left(\sqrt{u^2+2}+u\right)\left(\sqrt{u^2+2}-u\right)=2\\\left(\sqrt{v^2-2v+3}+v-1\right)\left(\sqrt{v-2v+3}-v+1\right)=2\end{cases}}\)
Theo đề bài thì ta có:
\(\left(u+\sqrt{u^2+2}\right)\left(v-1+\sqrt{v^2-2v+3}\right)=2\)
Từ đây ta có hệ:
\(\hept{\begin{cases}\sqrt{u^2+2}-u=\sqrt{v^2-2v+3}+v-1\left(1\right)\\\sqrt{u^2+2}+u=\sqrt{v^2-2v+3}-v+1\left(2\right)\end{cases}}\)
Lấy (1) - (2) ta được: \(u+v=1\)
Ta có: \(u^3+v^3+3uv=1\)
\(\Leftrightarrow3uv+u^2-uv+v^2=1\)
\(\Leftrightarrow\left(u+v\right)^2=1\)(đúng)
\(\Rightarrow\)ĐPCM
Mất 1 tiếng sau khi nhìn cái đề mới giải đc
Ta có \({u+v}≥ 2uv\)
\(=>{(u+v)^2-2uv}≥2uv\)
\(<=>{(u+v)^2/ 2}≥ 2uv\)
Và \({(u+v)^2/4}≥uv\)
\(P= {u^2+v^2}+{33 \over uv}\)
\(≥ {2uv}+{33\over uv}\)
\(={(u+v)^2 \over 2}+{33/{(u+v)^2 \over 4}}\)
Thế số vào ta sẽ đc kết quả \({65 \over 4}\)
Vậy GTNN của P là 65/4 khi u=v = 2
Sai!
Ta có \(P=u^2+v^2+\frac{33}{uv}\)
\(\ge\frac{\left(u+v\right)^2}{2}+\frac{33}{\frac{\left(u+v\right)^2}{4}}\)
\(=\frac{4^2}{2}+\frac{33}{\frac{4^2}{4}}=\frac{65}{4}\)
"=" <=> u=v=2