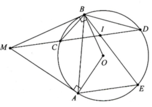
Cho đường tròn (O) đường kính AB. Trên tiếp tuyến Ax của đường tròn (O) lấy điểm M. Về cát tuyến MCD tới đường tròn (O) (C nằm giữa M và D, tia MD nằm giữa
hai ta MO và MÀ). Gọi I là trung điểm của đoạn thẳng CD.
a) Chúng mình tử giác MAIO nội tiếp. b) Ching minh MC. MD= AM²

Vì Ax là tia tt của (O)
`=>hat{MAO}=90^o`
Xét (O):
I là trung điểm CD
`=>OI bot CD`
`=>hat{OIM}=90^p`
Xét AMOI có:
`hat{MAO}=hat{OIM}=90^o`
`=>` tg MAIO nt(2 đỉnh nhìn nhau dưới 1 góc không đổi)
b)Xét (O) có:
`hat{ACM}=hat{ADC}`(2 góc nt và góc tạo bởi tia tt và dây cung cùng chắn 1 cung)
Xét tam giác AMD và tam giácACM ta có:
`hat{ADM}` chung
`hat{ACM}=hat{ADC}`(CMT)
`=>DeltaAMD~DeltaACM(gg)`
`=>(AM)/(MD)=(MC)/(AM)`
`=>AM^2=MD.MC`