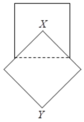
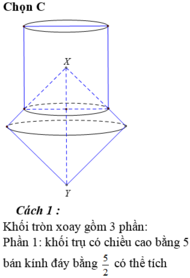
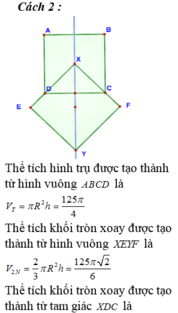
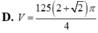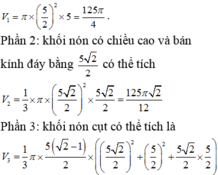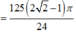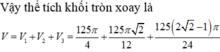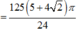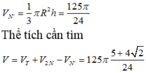Năm hình vuông xếp cạnh nhau sao cho một số đỉnh của chúng cùng nằm
trên một đường thẳng và hai hình vuông gần nhau thì chung đỉnh. Giả sửhai hình vuông nghiêng có diện tích là x cm2 và y cm2 còn ba hình vuông còn lại có diện tích lần lượt là 3 cm2, 5 cm2 và 10 cm2 Hãy tính tổng diệntích x + y.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 7 2015
bạn cũng có thể tham khảo cách giải này, đây là đề thi violympic cấp quốc gia đúng không
Hình vuông được chia thành 16 hình tam giác nhỏ bằng nhau (không chứng minh).
- Hình tam giác đơn có 16 hình
- Hình tam giác đôi có 8 hình.
- Hình tam giác tứ có 4 hình.
- Hình tam giác bát có 4 hình.
Vậy tổng diện tích của tất cả các tam giác so với 1 tam giác nhỏ bằng:
16x1 + 8x2 + 4x4 + 4x8 = 80 tam giác nhỏ
Tổng diện tích các hình tam giác gấp diện tích hình vuông số lần là:
80 : 16 = 5 lần
Vậy tổng diện tích các hình tam giác sẽ là:
156,25 x 5 = 781,25 cm2
ĐS: 781,25 (cm2)
29 tháng 3 2016
Giải:
Hình vuông được chia thành 16 hình tam giác nhỏ bằng nhau (không chứng minh).
- Hình tam giác đơn có 16 hình
- Hình tam giác đôi có 8 hình.
- Hình tam giác tứ có 4 hình.
- Hình tam giác bát có 4 hình.
Vậy tổng diện tích của tất cả các tam giác so với 1 tam giác nhỏ bằng:
16x1 + 8x2 + 4x4 + 4x8 = 80 tam giác nhỏ
Tổng diện tích các hình tam giác gấp diện tích hình vuông số lần là:
80 : 16 = 5 lần
Vậy tổng diện tích các hình tam giác sẽ là:
156,25 x 5 = 781,25 cm2
ĐS: 781,25 (cm2)
10 tháng 1 2023
a:
| GT | góc AOB và góc COD là hai góc đối đỉnh |
| KL | góc AOB=góc COD |
b:
| GT | a\(\perp\)b, c\(\perp\)b |
| KL | a//c |
4 tháng 6 2018
giúp mình với nhé, mình đang gấp lắm, ai giải bài rõ rang và nhanh nhất mình sẽ k cho,
DD
Đoàn Đức Hà
Giáo viên
27 tháng 5 2021
Diện tích mỗi hình vuông là:
\(4\times4=16\left(cm^2\right)\)
Phần diện tích giao nhau của hai hình vuông là:
\(16\div4=4\left(cm^2\right)\)
