Cho biêủ thức P= 2a2n+1 - 3a2n + 5a2n+1 - 7a2n + 3a2n+1 ( n là số tự nhiên ). Với giá trị nào của a thì P > 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a. Ta có \(63=3^2.7\) có 2 ước nguyên tố là 3 và 7
Do \(3n+1\) ko chia hết cho 3 với mọi n tự nhiên
\(\Rightarrow\) Phân số đã cho rút gọn được khi \(3n+1\) và 63 có ước chung là 7
\(\Rightarrow3n+1⋮7\)
Mà 3n+1 và 7 đều chia 3 dư 1 \(\Rightarrow3n+1=7\left(3k+1\right)\Rightarrow n=7k+2\) với k là số tự nhiên
Vậy \(n=7k+2\) với k là số tự nhiên thì phân số đã cho rút gọn được
b.
A là số tự nhiên khi \(63⋮3n+1\Rightarrow3n+1=Ư\left(63\right)\)
Mà \(3n+1⋮̸3\Rightarrow\left[{}\begin{matrix}3n+1=7\\3n+1=1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}n=2\\n=0\end{matrix}\right.\)

)
phần A.
63=3.3.7
A rút gọn được khi 63 và 3n+1 có chung ít nhất một ước 3 hoặc 7 ; nói cách khác để phân số rút gọn được thì 3n+1 phải chia hết cho 3 hoặc 7
Gọi a thuộc N
TH1: 3n+1=3a=> n = a - 1/3 loại vì n thuộc N
TH2: 3n+1=7a=> 3n+1|7 <=> 3(n-2)+7|7 <=>n-2|7=>n-2=0,7,14,28...=>n=2,9,16,30....
phần B
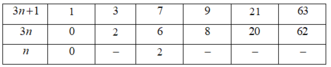
A=63/3n+1 là số tự nhiên khi 63 là ước của 3n+1 => 3n+1=3,7,9,21,63 => n= 2, 20 (loại các trường hợp cho n khác số tự nhiên)

A)Để A được rút gọn thì 3n+1 là ước của 63
=>3n + 1 thuộc {63;-1;1;-63}
=>n thuộc ...
b|) Tương tự

Gọi d là ước nguyên tố của 63 và 3n+1
Ta có 63 : d ( mình dùng dấu chia thay cho chia hết)
=>d=7
Vậy 3n+1 : 7
=>3n+1-7 :7
3n-6 :7
3(n-2) :7
Mà (3;7)=1
=>n-2 :7
=>n-2=7k
n=7k+2
Vậy để A rút gọn được thì n=7k+2
Để A là STN thì 63 : 3n+1
=>3n+1 thuộc Ư(63)={1;3;7;9;21;63}
Bạn tự tìm nốt nha

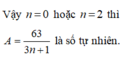
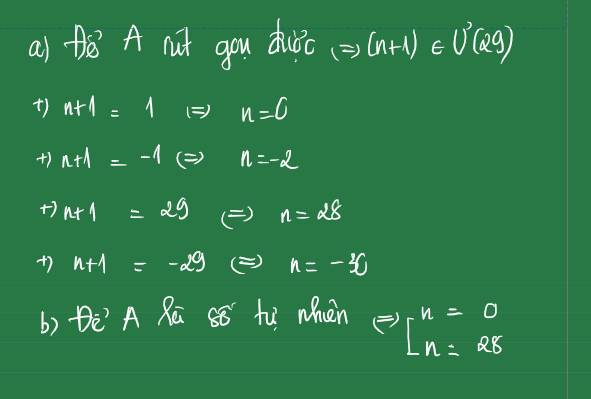
Ta có:
\(P=2a^{2n+1}-3a^{2n}+5a^{2n+1}-7a^{2n}+3a^{2n+1}\)
\(P=\left(2a^{2n+1}+5a^{2n+1}+3a^{2n+1}\right)+\left(-3a^{2n}-7a^{2n}\right)\)
Suy ra: \(P=10a^{2n+1}+\left(-10a\right)^{2n}\)
Mà \(2n⋮2\)còn \(2n+1\)ko chia hết cho 2
Do đó: \(a>0\)thì P>0
Nhầm cái chỗ suy ra:
\(P=10a^{2n+1}+\left(-10\right)a^{2n}\)