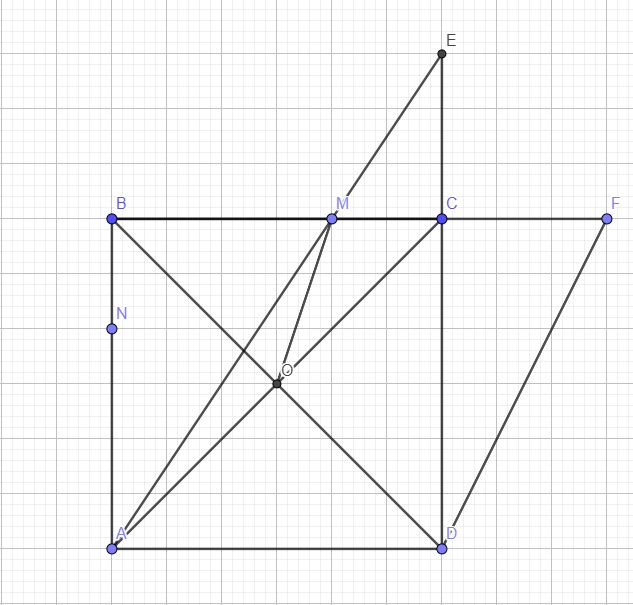
1/ Trên cạnh BC của hình vuông ABCD có 4 cạnh =6, lấy điểm E sao cho BE = 2. Trên tia đối của tia CD lấy F sao cho CF = 3. Gọi M là giao điểm của AE và BF. Tính AMC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


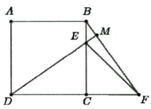
Chứng minh được:
C B F ^ + B E M ^ = M D F ^ + D E C ^ = 90 0
=> B M D ^ = 90 0 nên M thuộc đường tròn đường kính BD. Mà E Î BC nên quỹ tích của điểm M là là cung B C ⏜ của đường tròn đường kính BD

@Vũ Minh Tuấn @Lê Thị Thục Hiền @Trần Thanh Phương

Đặt cạnh hình vuông là a, ta có \(BD=\sqrt{a^2+a^2}=a\sqrt{2}\)
\(\Rightarrow BO=\dfrac{1}{2}BD=\dfrac{a\sqrt{2}}{2}\Rightarrow BO.BD=a^2\)
Xét 2 tam giác vuông AED và MAB có:
\(\left\{{}\begin{matrix}\widehat{ADE}=\widehat{MBA}=90^0\\\widehat{AED}=\widehat{MAB}\left(slt\right)\end{matrix}\right.\) \(\Rightarrow\Delta AED\sim\Delta MAB\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{BM}=\dfrac{ED}{AB}\Rightarrow BM.ED=AD.AB=a^2\)
\(\Rightarrow BM.ED=BO.BD\)
Mà \(ED=BF\) (do \(BC=CD\) và \(CE=CF\))
\(\Rightarrow BM.BF=BO.BD\Rightarrow\dfrac{BM}{BD}=\dfrac{BO}{BF}\)
Xét hai tam giác BOM và BFD có:
\(\left\{{}\begin{matrix}\dfrac{BM}{BD}=\dfrac{BO}{BF}\\\widehat{OBM}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta BOM\sim\Delta BFD\left(c.g.c\right)\)