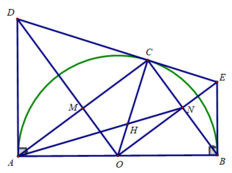
Trên nửa đường tròn (O;R) đường kính BC, lấy điểm A sao cho BA = R.
a) Chứng minh tam giác ABC vuông tại A và tính số đo các góc B, C của tam giác vuông ABC.
b) Qua B kẻ tiếp tuyến với nửa đường tròn (O), nó cắt tia CA tại D. Qua D kẻ tiếp tuyến DE với nửa đường tròn (O) (E là tiếp điểm). Gọi I là giao điểm của OD và BE. Chứng minh rằng OD\(\perp\)BE và DI.DO = DA.DC
c) Kẻ EH vuông góc với BC tại H. EH cắt CD tại G. Chứng minh IG song song với BC.

a: Xét (O) có
ΔABC nội tiếp
BC là đường kính
Do đó: ΔABC vuông tại A
Xét ΔBCA vuông tại A có sin ACB=AB/BC=1/2
nên góc ACB=30 độ
=>góc ABC=60 độ
b: Xét (O) có
DB,DE là các tiếp tuyến
nên DB=DE
mà OB=OE
nên OD là đường trung trực của BE
=>OD vuông góc với BE
DI*DO=DB^2
DA*DC=DB^2
Do đó: DI*DO=DA*DC