Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

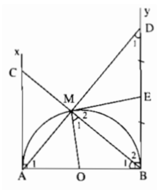
Tam giác EBM cân nên ∠ M 2 = ∠ B 2 . Suy ra ∠ M 1 + ∠ M 2 = ∠ B 1 + ∠ B 2 = 90 ° , tức là ME ⊥ OM tại M. Vậy ME là tiếp tuyến của nửa đường tròn.

a: Xét (O) có
CA,CM là tiếp tuyến
nênCA=CM và OC là phân giác của góc AOM(1)
mà OA=OM
nên OC là trung trực của AM
=>OC vuông góc với AM
Xét (O) có
DM,DB là tiếp tuyến
nên DM=DB và OD là phân giác của góc MOB(2)
Xét (O)có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
=>MB vuông góc MA
=>MB//OC
b: Từ (1), (2) suy ra góc COD=1/2*180=90 độ
=>OC vuông góc với OD
mà OM vuông góc DC
nên MC*MD=OM^2
=>AC*BD=R^2
c: Gọi H là trung điểm của CD
Xét hình thang ABDC có
H,O lần lượtlà trung điểm của CD,AB
nên HO là đường trung bình
=>HO//AC//BD
=>HO vuông góc với AB
=>AB là tiếp tuyến của (H)

a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Xét ΔADB vuông tại A có AC là đường cao
nên \(AD^2=DB\cdot DC\)
b: Xét (O) có
EC là tiếp tuyến
EA là tiếp tuyến
Do đó: EC=EA
=>ΔECA cân tại C
=>góc ECA=góc EAC
\(\Leftrightarrow90^0-\widehat{ECA}=90^0-\widehat{EAC}\)
hay \(\widehat{EDC}=\widehat{ECD}\)
=>ΔECD cân tại E
=>ED=EC
mà EC=EA
nên EA=ED
hay E là trung điểm của AD
a: Xét (O) có
CM,CA là các tiếp tuyến
nên CM=CA và OC là phân giác của góc MOA(1)
mà OM=OA
nên OC là đường trung trực của MA
=>OC vuông góc với MA tại I
Xét (O) có
DM,DB là các tiếp tuyến
nên DM=DB và OD là phân giác của góc MOB(2)
mà OM=OB
nên OD là trung trực của BM
=>OD vuông góc với BM
Từ (1) và (2) suy ra góc COD=1/2*180=90 độ
=>O nằm trên đường tròn đường kính CD
b: Xét tứ giác MIOK có
góc MIO=góc IOK=góc MKO=90 độ
nên MIOK là hình chữ nhật
=>MO=IK
c: Xét hình thang ABDC có
O,O' lần lượt là trung điểm của AB,CD
nên OO' là đường trung bình
=>OO''//AC
=>OO' vuông góc với AB
=>AB là tiếp tuyến của (O')