Trong không gian với hệ tọa độ Oxyz cho hai điểm M(1;2;3), N(3;4;5) và mặt phẳng P : x + 2 y + 3 z - 14 = 0 . Gọi ∆ là đường thẳng thay đổi nằm trong mặt phẳng (P). Gọi H, K lần lượt là hình chiếu vuông góc của M, N trên ∆ . Biết rằng khi M H = N K thì trung điểm của HK luôn thuộc một đường thẳng d cố định, phương trình của đường thẳng d là
A. x = 1 y = 13 - 2 t z = - 4 + t
B. x = t y = 13 - 2 t z = - 4 + t
C. x = t y = 13 + 2 t z = - 4 + t
D. x = t y = 13 - 2 t z = - 4 - t

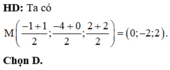
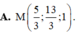
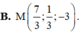
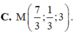


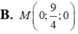
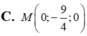


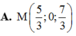
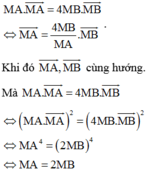


Do đó J thuộc mặt phẳng trung trực của MN là x + y + z - 9 = 0
Lại có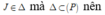
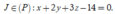
Từ đó suy ra J thuộc giao tuyến của hai mặt phẳng có phương trình
Chọn B.