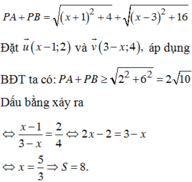Tìm trên trục hoành Ox điểm P sao cho tổng các khoảng cách từ P đến các điểm A và B là nhỏ
nhất (hay( PA+PB)min ). Biết rằng:
a/A (1;1) , B (2; -4) b/ A (1;2) , B (3;4)
HD: a/ A, B khác phía Ox => Po(x;0) = Ox ∩ AB . A, Po, B thẳng hàng=> Po(\(\dfrac{6}{5}\);0) \(\equiv\) P
b/ A, B cùng phía Ox. Lấy A1 đối xứng với A qua Ox ⇒A1 (1; -2) => P\(\equiv\) Po (\(\dfrac{5}{3}\);0)