Câu 1 : Tìm GTNN của hàm số \(y=x^3-3x+5\) trên đoạn [0;2]
A. 5 B. 3 C. 7 D. 2
Câu 2 : Tìm GTLN của hàm số \(y=x^4-4x^2-3\) trên [ -2 ; 1]
A. -3 B. -6 C. -7 D. 1
Câu 3 :Tìm GTLN của hàm số \(y=\frac{x^2+3x}{x-1}\) trên khoảng \(\left(-\infty;0\right)\)
A. 1 B. 0 C. 9 D. 2
Câu 4 : Tìm tổng GTLN và GTNN của hàm số \(y=\frac{2x+1}{x^2+2}\) trên \(\left(-\infty;+\infty\right)\)
A. \(\frac{-1}{2}\) B. 1 C. \(\frac{1}{2}\) D. \(\frac{3}{2}\)

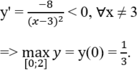

1.
\(y'=3x^2-3=0\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
\(y\left(0\right)=5;\) \(y\left(1\right)=3;\) \(y\left(2\right)=7\)
\(\Rightarrow y_{min}=3\)
2.
\(y'=4x^3-8x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-\sqrt{2}\end{matrix}\right.\)
\(f\left(-2\right)=-3\) ; \(y\left(0\right)=-3\) ; \(y\left(-\sqrt{2}\right)=-7\) ; \(y\left(1\right)=-6\)
\(\Rightarrow y_{max}=-3\)
3.
\(y'=\frac{\left(2x+3\right)\left(x-1\right)-x^2-3x}{\left(x-1\right)^2}=\frac{x^2-2x-3}{\left(x-1\right)^2}=0\Rightarrow x=-1\)
\(y_{max}=y\left(-1\right)=1\)
4.
\(y'=\frac{2\left(x^2+2\right)-2x\left(2x+1\right)}{\left(x^2+2\right)^2}=\frac{-2x^2-2x+4}{\left(x^2+2\right)^2}=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
\(y\left(1\right)=1\) ; \(y\left(-2\right)=-\frac{1}{2}\Rightarrow y_{min}+y_{max}=-\frac{1}{2}+1=\frac{1}{2}\)