Cho (P):y=ax2+bx+c
a)Tìm (P) qua A(0;2) đỉnh S(1;1)
b)Lập BBT và tìm GTNN của (P)
c)Tìm m để (d):y=2x+m cắt (P) từ 2 điểm phân biệt
{ GIÚP VỚI NHÉ,CẦN GẤP}
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LK
1
R
26 tháng 11 2021
THam khảo
Bài 2:
Ta có: −Δ4a=−3−Δ4a=−3
⇔−Δ=−12a⇔−Δ=−12a
⇔b2−4a=12a⇔b2−4a=12a
⇔b2−16a=0(1)⇔b2−16a=0(1)
Thay x=-1 và y=6 vào (P), ta được:
a⋅(−1)2+b(−1)+1=6a⋅(−1)2+b(−1)+1=6
⇔a−b=5⇔a−b=5
⇔a=b+5⇔a=b+5(2)
Thay (2) vào (1), ta được:
b2−16(b+5)=0b2−16(b+5)=0
⇔b2−16b+64−144=0⇔b2−16b+64−144=0
⇔(b−8)2=144⇔(b−8)2=144
⇔[b=20b=−4⇔[a=25a=1
VN
1
20 tháng 12 2020
Do (p) đi qua A(0;3), B(3;0) và C(-1;1) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}3=c\\9a+3b+c=0\\a+b+c=-1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}c=3\\3a+b=-1\\a+b=-4\end{matrix}\right.\\ \Leftrightarrow \left\{{}\begin{matrix}c=3\\a=\dfrac{3}{2}\\b=\dfrac{-11}{2}\end{matrix}\right.\)
NP
1
CM
3 tháng 4 2018
Vì parabol đi qua ba điểm A, B, C nên ta có hệ phương trình:
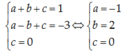
Vậy (P): y = -x2 + 2x
Chọn C.
8 tháng 12 2021
Theo đề, ta có:
\(\left\{{}\begin{matrix}-\dfrac{b}{2a}=2\\-\dfrac{b^2-4ac}{4a}=1\\16a+4b+c=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-4a\\16a^2-4ac=-4a\\16a-16b+c=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}c=5\\16a^2+4a-20=0\\b=-4a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}c=5\\16a^2+20a-16a-20=0\\b=-4a\end{matrix}\right.\)
Đến đây bạn tự làm tiếp được rồi
