Tìm hình chiếu vuông góc của điểm M ( 3;1) trên đường thẳng \(\Delta:\left\{{}\begin{matrix}x=-2-2t\\y=1+2t\end{matrix}\right.\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì M’ là hình chiếu vuông góc của điểm M trên trục Ox nên M’(3 ;-2 ;-5)
Đáp án B

Chọn A.
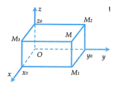
Với M(a, b, c) thì hình chiếu vuông góc của M lên mặt phẳng (Oxy) là M_1(a;b;0)
Do đó,hình chiếu của điểm M(1;2;-3) lên mặt phẳng (Oxy) là điểm M’(1;2;0).

Chọn A.
Với M (a,b,c) thì hình chiếu vuông góc của M lên mặt phẳng (Oxy) là M1(a;b;0)
Do đó, hình chiếu của điểm M(1;2;-3) lên mặt phẳng (Oxy) là điểm M’(1;2;0).

Đáp án A.
Tọa độ điểm M 2 ; − 1 ; 1 trên mặt phẳng (Oxy) là M ' 2 ; − 1 ; 0 .

Vecto pháp tuyến của mp α là n → =(2;-1;2), H là hình chiếu vuông góc của M trên mp α nên M H ⊥ m p α , đường thẳng MK có vecto pháp tuyến n → = ( 2 ; - 1 ; 2 )
Ta có pt tham số của đường thẳng MH là : x = 1 + 2 t y = - 1 - t z = 2 + 2 t
Thay x,y,z từ pt tham số của đường thẳng MH và pt mp α , ta có:
2(1+2t)-(-1-t)+2(2+2t)+11=0 <=> t=-2
Vậy H(-3;1;-2)





VTCP của \(\Delta\) là \(\overrightarrow{u}=\left(-2;2\right)=2\left(-1;1\right)\).
Gọi \(H\) là hình chiếu vuông góc của \(M\) trên \(\Delta\)
\(\Rightarrow\Delta\) vuông góc \(MH\) \(\Rightarrow\overrightarrow{u}.\overrightarrow{MH}=0\)
Do \(H\in\Delta\Rightarrow H\left(-2-2t;1+2t\right)\Rightarrow\overrightarrow{MH}=\left(-5-2t;2t\right)\)
Ta có: \(\overrightarrow{u}.\overrightarrow{MH}=0\Leftrightarrow-1\left(-5-2t\right)+1.2t=0\Leftrightarrow5+4t=0\Leftrightarrow t=-\dfrac{5}{4}\)
\(\Rightarrow H\left(\dfrac{1}{2};-\dfrac{3}{2}\right)\).