Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Với M(a, b, c) thì hình chiếu vuông góc của M lên mặt phẳng (Oxy) là M_1(a;b;0)
Do đó,hình chiếu của điểm M(1;2;-3) lên mặt phẳng (Oxy) là điểm M’(1;2;0).

Gọi tọa độ M(x;y;z)
Ta có: \(\overrightarrow{AB}\) = (2; -2; -8)
\(\overrightarrow{AM}\)=( x+1; y-2; z-3)
A, B, M thẳng hàng khi: \(\left[\overrightarrow{AB};\overrightarrow{AM}\right]\)=\(\overrightarrow{0}\) ⇔ \(\left\{{}\begin{matrix}-2z+8y-10=0\\-8x-2z-2=0\\2y+2x-2=0\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}x=0\\y=1\\z=-1\end{matrix}\right.\)
=> Câu D đúng

Chọn D
Ta có x + my + (2m + 1)z – m – 2 = 0 <=> m(y + 2z -1) + x + z - 2 = 0 (*)
Phương trình (*) có nghiệm với 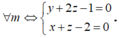
Suy ra (P) luôn đi qua đường thẳng 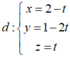
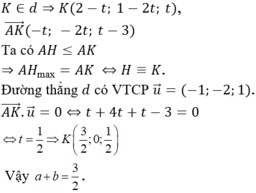

Đáp án A
Phương pháp:
Hình chiếu vuông góc của điểm M ( x 0 ; y 0 ; z 0 ) trên mặt phẳng (Oxy) là điểm M ' ( x 0 ; y 0 ; z 0 )
Cách giải:
Hình chiếu vuông góc của điểm A(1;2;3) trên mặt phẳng (Oxy) là điểm N(1;2;0)

Đáp án C
Hình chiếu vuông góc của M(2;-1;4) lên mặt phẳng (Oxy) là điểm H(2;-1;0).

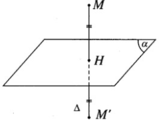
Phương trình tham số của đường thẳng ∆ đi qua điểm M(1; -1; 2) và vuông góc với mặt phẳng ( α ): 2x – y + 2z + 12 = 0 là:
Δ 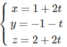
Xét điểm H(1 + 2t; -1 – t; 2 + 2t) ∈ ∆
Ta có H ∈ ( α ) ⇔ 2(1 + 2t) + (1 + t) + 2(2 + 2t) + 12 = 0 ⇔ t = −19/9
Vậy ta được ![]()

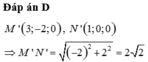
Chọn A.
Với M (a,b,c) thì hình chiếu vuông góc của M lên mặt phẳng (Oxy) là M1(a;b;0)
Do đó, hình chiếu của điểm M(1;2;-3) lên mặt phẳng (Oxy) là điểm M’(1;2;0).