Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(0;1;0), B(2;2;2), C(-2;3;1) và đường thẳng d : x - 1 2 = y + 2 - 1 = z - 3 2 . Tìm điểm M thuộc d để thể tích V của tứ diện MABC bằng 3.
A. M 1 - 15 2 ; 9 4 ; - 11 2 , M 2 - 3 2 ; - 3 4 ; 1 2
B. M 1 - 3 5 ; - 3 4 ; 1 2 , M 2 - 15 2 ; 9 4 ; 11 2
C. M 1 3 2 ; - 3 4 ; 1 2 , M 2 15 2 ; 9 4 ; 11 2
D. M 1 3 5 ; - 3 4 ; 1 2 , M 2 15 2 ; 9 4 ; 11 2

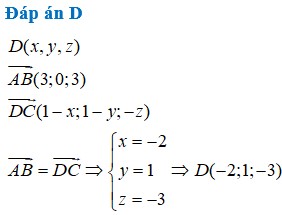
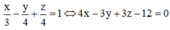





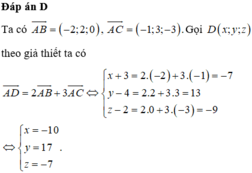

Đáp án A
Ta có A B → = 2 ; 1 ; 2 A C → = - 2 ; 2 ; 1 ⇒ A B → ; A C → = - 3 ; - 6 ; 6 ⇒ S ∆ A B C = 1 2 A B → , A C → = 9 2
Phương trình mặt phẳng (ABC) là - 3 x - 0 - 6 y - 1 + 6 z - 0 = 0 ⇔ x + 2 y - 2 z - 2 = 0
Điểm M ∈ d ⇒ M 2 t + 1 ; - t - 2 ; 2 t + 3 ⇒ d M , A B C = 4 t + 11 3 1
Lại có V M . A B C = 1 3 d M , A B C . S ∆ A B C ⇒ d M , A B C = 2 2
Từ (1) và (2) suy ra 4 t + 11 3 = 2 ⇔ 4 t + 11 = 6 ⇔ [ t = - 5 4 t = - 17 4 . Vậy [ M 1 - 15 2 ; 9 4 ; - 11 2 M 2 - 3 2 ; - 3 4 ; 1 2 .