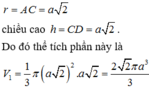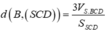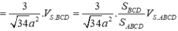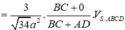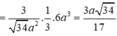Cho hình thang ABCD có AD // BC và AD=2BC ,B(4;0) phương trình đường chéo AC là 2x-y-3=0 trung điểm E của AD thuộc đường thẳng d:x-2y+10=0.Tìm tọa độ các đỉnh còn lại của hình thang biết cot ADC bằng 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 1 2021
Bài làm:
a) Do BC//AD và AD\(\subset\) (SAD)
=> BC// (SAD)
b) có \(\dfrac{DE}{AE}=\dfrac{DN}{NS}=2\)
=> NE//SA
do BC//AD => \(\dfrac{BC}{AD}=\dfrac{OB}{OD}=\dfrac{1}{2}\) => \(\dfrac{DE}{AE}=\dfrac{OD}{OB}=2\) => OE//AB
Do NE//SA và OE//AB mà OE,NE \(\subset\)(ONE); SA,SB\(\subset\) (SAB)
=> (ONE) //(SAB)
CM
19 tháng 7 2018
Đáp án C
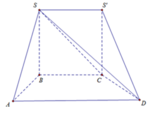
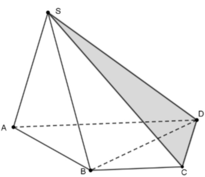
Ta có V D . S S ' C = V D . S C B = V S . B C D
Mặt khác S B C D = 1 2 S A B D = 1 3 S A B C D
Do đó V D . S S ' C = V D . S C B = V S . B C D = 1 3 V S . A B C D
Khi đó V S S ' A B C D V S . A B C D = 1 3 + 1 1 = 4 3
CM
12 tháng 8 2018
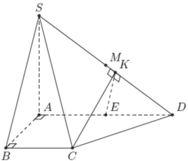
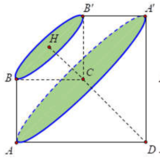
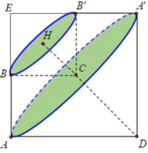
Ta có A E = B C A E / / B C suy ra AECB là hình bình hành. Do A B C ^ = 90 0 nên AECB là hình chữ nhật.
Suy ra C E ⊥ A D mà S A ⊥ C E ⇒ C E ⊥ S A D ⇒ C E ⊥ S D .
Ta lại có E K ⊥ S D ⇒ S D ⊥ E K M ⇒ S D ⊥ C K .
Suy ra góc giữa hai mặt phẳng (SAD) và (SCD) là góc EKC
CM
3 tháng 1 2020
Chọn đáp án A.
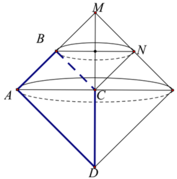
Gọi M là giao điểm của AB và CD. Từ B kẻ đường thẳng song song với AC, cắt CM tại N.
Khi quay ABCD quanh trục CD ta được hai phần:
+ Tam giác ACD sinh ra khối nón với bán kính đáy
