Phương trình có hai nghiệm phân biệt là x1 ; x2. Tính giá trị của biểu thức P = log3x1+ log27x2 biết x1< x2.
A. P= 0
B. P =1
C. 8 3
D. 1 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:
\(\text{Δ}=\left(m-1\right)^2-4\left(-2m-1\right)\)
\(=m^2-2m+1+8m+4=m^2+6m+5\)
Để (1) vô nghiệm thì (m+1)(m+5)<0
hay -5<m<-1
Để (1) có nghiệm thì (m+1)(m+5)>=0
=>m>=-1 hoặc m<=-5
Để (1) có hai nghiệm phân biệt thì (m+1)(m+5)>0
=>m>-1 hoặc m<-5
b: Để (1) có hai nghiệm phân biệt cùng dương thì
\(\left\{{}\begin{matrix}\left[{}\begin{matrix}m>-1\\m< -5\end{matrix}\right.\\m>1\\m< -\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow m\in\varnothing\)
c. Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m-1\\x_1x_2=-2m-1\end{matrix}\right.\)
\(x_1^2+x_2^2=3\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=3\)
\(\Leftrightarrow\left(m-1\right)^2+2\left(2m+1\right)=3\)
\(\Leftrightarrow m^2+2m=0\Rightarrow\left[{}\begin{matrix}m=0\\m=-2\left(loại\right)\end{matrix}\right.\)

`a)ac=-3<0`
`=>b^2-4ac>0`
`=>` phương trình luôn có hai nghiệm phân biệt với mọi m
`b)` áp dụng vi-ét:`x_1+x_2=m,x_1.x_2=-3`
`(x_1+6).(x_2+6) = 2019`
`<=>x_1.x_2+6(x_1+x_2)+36=2019`
`<=>6m-3+36=2019`
`<=>6m+33=2019`
`<=>6m=1986`
`<=>m=331`
Vậy `m=331` thì `(x_1+6).(x_2+6) = 2019`

`a)ac=-3<0`
`=>b^2-4ac>0`
`=>` phương trình luôn có hai nghiệm phân biệt với mọi m
`b)` áp dụng vi-ét:`x_1+x_2=m,x_1.x_2=-3`
`(x_1+6).(x_2+6) = 2019`
`<=>x_1.x_2+6(x_1+x_2)+36=2019`
`<=>6m-3+36=2019`
`<=>6m+33=2019`
`<=>6m=1986`
`<=>m=331`
Vậy `m=331` thì `(x_1+6).(x_2+6) = 2019`

a,ta có \(\Delta\)=\(\left(-m\right)^2-4.\left(-3\right)=m^2+12\)
vì \(m^2\ge\)0(\(\forall\)m)=>\(m^2+12\ge12=>m^2+12>0=>\Delta>0\)
vậy pt luôn có 2 nghiệm phân biệt với mọi m
b, theo vi ét=>\(\left\{{}\begin{matrix}x1+x2=m\\x1.x2=-3\end{matrix}\right.\)
có \(\left(x1+6\right).\left(x2+6\right)=2019< =>x1.x2+6x1+6x2+36-2019=0< =>-3+6\left(x1.x2\right)-1983=0< =>6m=1986< =>m=\dfrac{1986}{6}=331\)

\(\Delta=\left(m+3\right)^2-4\left(m+2\right)=m^2+6m+9-4m-8=m^2+2m+1=\left(m+1\right)^2\)
Để pt có 2 nghiệm pb khi \(m+1\ne0\Leftrightarrow m\ne-1\)
Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=m+3\left(1\right)\\x_1x_2=m+2\left(2\right)\end{matrix}\right.\)Lại có \(x_1-x_2=-1\)(3)
Từ (1) ; (3) ta có hệ \(\left\{{}\begin{matrix}x_1+x_2=m+3\\x_1-x_2=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x_1=m+2\\x_2=m+3-x_1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{m+2}{2}\\x_2=\dfrac{2m+6-m-2}{2}=\dfrac{m+4}{2}\end{matrix}\right.\)
Thay vào (2) ta được
\(\dfrac{\left(m+2\right)\left(m+4\right)}{4}=m+2\Leftrightarrow\left(m+2\right)\left(m+4\right)-4\left(m+2\right)=0\)
\(\Leftrightarrow\left(m+2\right)m=0\Leftrightarrow m=0\left(tm\right);m=-2\left(ktm\right)\)

a) Ta có: \(\Delta=\left(-4\right)^2-4\cdot1\cdot\left(2m-3\right)=16-4\left(2m-3\right)\)
\(\Leftrightarrow\Delta=16-8m+12=-8m+28\)
Để phương trình có hai nghiệm x1;x2 phân biệt thì \(-8m+28>0\)
\(\Leftrightarrow-8m>-28\)
hay \(m< \dfrac{7}{2}\)
Với \(m< \dfrac{7}{2}\) thì phương trình có hai nghiệm phân biệt x1;x2
nên Áp dụng hệ thức Viet, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-\left(-4\right)}{1}=4\\x_1\cdot x_2=\dfrac{2m-3}{1}=2m-3\end{matrix}\right.\)
Để phương trình có hai nghiệm x1,x2 phân biệt thỏa mãn tổng 2 nghiệm và tích hai nghiệm là hai số đối nhau thì
\(\left\{{}\begin{matrix}m< \dfrac{7}{2}\\4+2m-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{7}{2}\\2m+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{7}{2}\\2m=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{7}{2}\\m=-\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow m=-\dfrac{1}{2}\)
Vậy: Khi \(m=-\dfrac{1}{2}\) thì phương trình có hai nghiệm x1,x2 phân biệt thỏa mãn tổng 2 nghiệm và tích hai nghiệm là hai số đối nhau
Điều kiện : x> 0
Ta có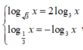
, khi đó phương trình đã cho trở thành
( log3x)2 - 4log3x+ 2log3x-3= 0 hay ( log3x)2 - 2log3x- 3= 0 (*)
Đặt t= log3x, suy ra phương trình (*) trở thành : t2- 2t-3= 0
Suy ra t= -1 hoặc t= 3
Với t= -1, ta được
Với t= 3 ta được log3x= 3 nên x2= 27
Từ đó ; P= log3x1+ log27x2 = log3 + log2727 = -1+ 1= 0
Chọn A