Cho hình thang ABCD vuông tại A và D . Biết AB=18 ; CD=32 , hai đường chéo AC và BD vuông góc với nhau . Tính AC, AD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 12 2015
chỉ cần chứng minh tam giác ABD đồng dạng tam giác DAC
==>\(\frac{AD}{DC}=\frac{AB}{AD}\)
==>\(AD^2=AB\cdot DC\)
LẮP VÀO TÍNH LÀ XONG
25 tháng 12 2015
Dân ta phải biết sử ta cái gì không biết thì tra google
Ai đồng ý thì tick mình cái
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 7 2021
Xét tam giác vuông OAB:
\(OB=\sqrt{AB^2-OA^2}=4\)
Áp dụng hệ thức lượng cho tam giác vuông ABD với đường cao AO:
\(AB^2=OB.BD\Rightarrow BD=\dfrac{AB^2}{OB}=13\)
\(\Rightarrow\left\{{}\begin{matrix}OD=BD-OB=9\\AD=\sqrt{BD^2-AB^2}=\sqrt{29}\end{matrix}\right.\)
\(\widehat{BAO}=\widehat{DCO}\left(slt\right)\Rightarrow\Delta_VAOB\sim\Delta_VCOD\) (g.g)
\(\Rightarrow\dfrac{AB}{DC}=\dfrac{OB}{OD}\Rightarrow DC=\dfrac{AB.OD}{OB}=\dfrac{9\sqrt{13}}{2}\)
\(S_{ABCD}=\dfrac{1}{2}AD.\left(AB+CD\right)=\dfrac{1}{2}.\sqrt{29}.\left(2\sqrt{13}+\dfrac{9\sqrt{13}}{2}\right)=...\)
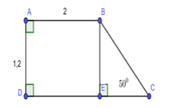
Dễ thấy :Tam giác OAB ~Tam giác OCD
=> AB/DC = OB/OD = OB.OD/OD^2 = AO^2/OD^2 (Hệ thức lượng trong tam giác)
=> AO/OD = căn(AB/CD)= căn(18/32) = 3/4
Ta có : tanADO = AO/DO = AB/AD
=> AB/AD = 3/4 <=> AD = 4AB/3 = 18.4/3 = 24 (cm)
AC=\(\sqrt{AD^2+DC^2}=40\)
tick nha