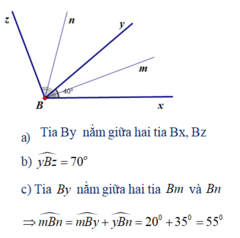
Cho góc xBy = 550. Trên các tia Bx; By lần lượt lấy các điểm A; C (A ≠ B; C ≠ B). Trên đoạn thẳng AC lấy điểm D sao cho góc ABD = 300
a. Tính độ dài AC, biết AD = 4cm, CD = 3cm.
b. Tính số đo của góc DBC.
c. Từ B vẽ tia Bz sao cho góc DBz = 900. Tính số đo góc ABz.

a. Ta có ; AC = AD +CD
\(\Rightarrow\)AC = 4 + 3
\(\Rightarrow\)AC = 7cm
b.góc DBC = góc ABC - góc ABD
\(\Rightarrow\widehat{DBC}=55^0-30^0=25^0\)
c.\(\widehat{ABz}=\widehat{DBz}-\widehat{ABD}\)
\(\Rightarrow\widehat{ABz}=90^0-30^0=50^0\)
Học tốt
a) Vì D thuộc đoạn thẳng AC nên ta có:
AC=AD+DC=4+3=7AC=AD+DC=4+3=7 (cm)
b) Do ˆxBy=55oxBy^=55o hay ˆABC=55oABC^=55o
Ta có BD, BC thuộc cùng một mặt phẳng bờ chưa tia BA
và có ˆABD=30o<ˆABc=55oABD^=30o<ABc^=55o
⇒BD⇒BD nằm giữa tia BA,BCBA,BC
⇒ˆABC=ˆABD+ˆDBC⇒ABC^=ABD^+DBC^
⇒ˆDBC=ˆABC−ˆABD=55o−30o=25o⇒DBC^=ABC^−ABD^=55o−30o=25o
c) Vì Bz,BABz,BA cùng thuộc một nửa mặt phẳng bờ chứa tia BDBD
Và có ˆDBz=90o>ˆDBA=30oDBz^=90o>DBA^=30o
⇒BA⇒BA nằm giữa tia BD,BzBD,Bz
⇒ˆDBz=ˆDBA+ˆABz⇒DBz^=DBA^+ABz^
⇒ˆABz=ˆDBz−ˆDBA=90o−ˆ30o=60o⇒ABz^=DBz^−DBA^=90o−30o^=60o.