bài 6: Cho tam giác ABC vuông tại A, góc B có số đo bằng 60 độ. Vẽ AH vuông góc với BC,(H thuộc BC)a) So sánh AB và AC; BH và HCb) Lấy điểm D thuộc tia đối của tia HA sao cho HD=HA. Chứng minh rằng: tam giác AHC= tam giác DHCc) Tính số đo của góc BDCCác bạn vẽ hình và ghi giải thiết kết luận với ạ em xin cảm...
Đọc tiếp
bài 6: Cho tam giác ABC vuông tại A, góc B có số đo bằng 60 độ. Vẽ AH vuông góc với BC,(H thuộc BC)
a) So sánh AB và AC; BH và HC
b) Lấy điểm D thuộc tia đối của tia HA sao cho HD=HA. Chứng minh rằng: tam giác AHC= tam giác DHC
c) Tính số đo của góc BDC
Các bạn vẽ hình và ghi giải thiết kết luận với ạ em xin cảm ơn
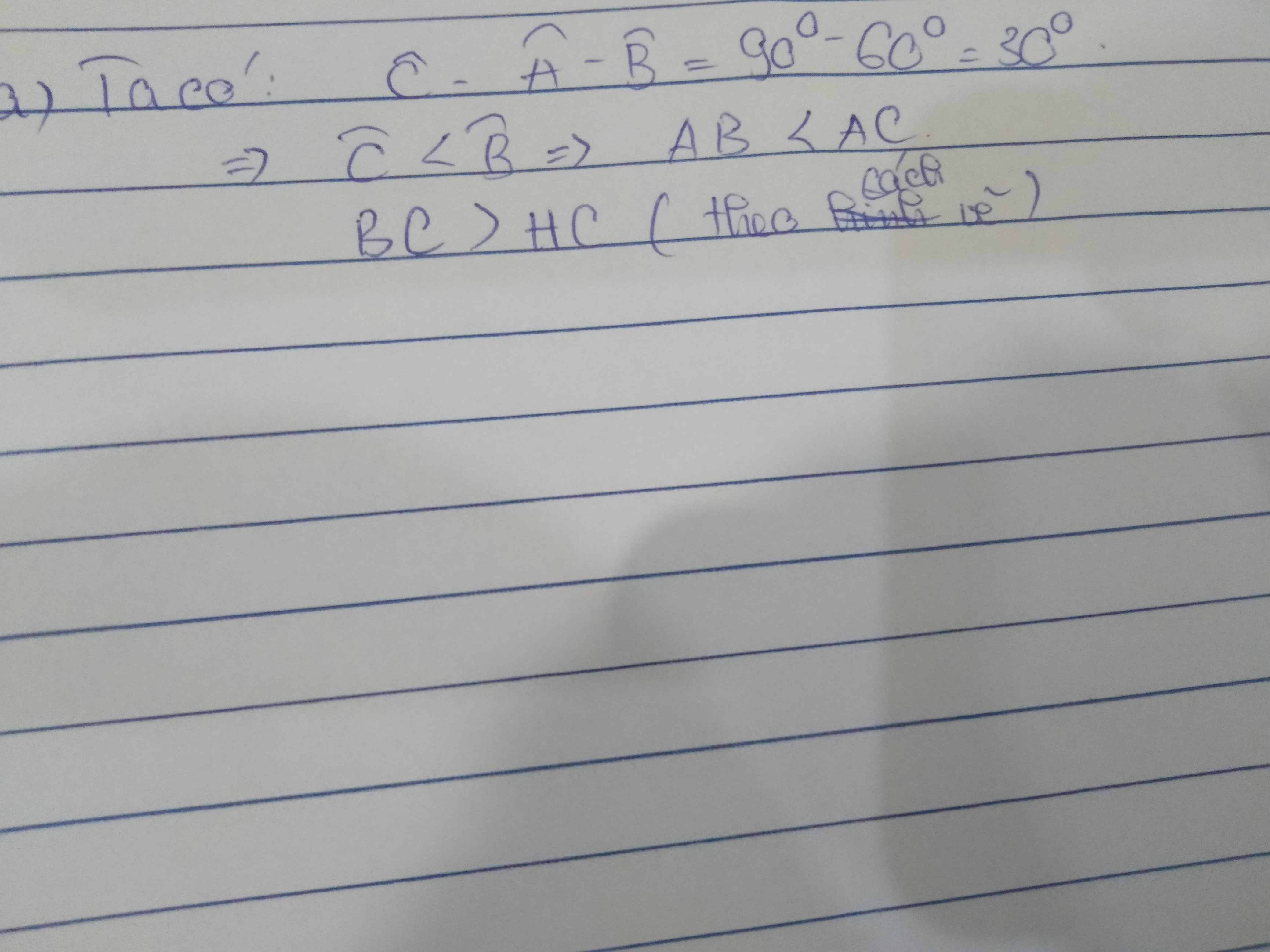
a: \(\widehat{C}=90^0-60^0=30^0\)
Xét ΔABC có \(\widehat{C}< \widehat{B}\)
nên AB<AC
Xét ΔABC có AB<AC
mà HB là hình chiếu của AB trên BC
và HC là hình chiếu của AC trên BC
nên HB<HC
b: Xét ΔAHC vuông tại H và ΔDHC vuông tại H có
HC chung
HA=HD
Do đó: ΔAHC=ΔDHC
c: Xét ΔBAC và ΔBDC có
CA=CD
\(\widehat{ACB}=\widehat{DCB}\)
CB chung
Do đó: ΔBAC=ΔBDC
Suy ra: \(\widehat{BAC}=\widehat{BDC}=90^0\)