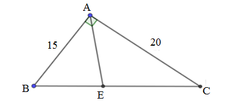
1. Cho tam giác ABC vuông tại A ,có AB=20cm; BC=25cm . Điểm M thuộc cạnh AB
a ) tính AC
b) Qua B vẽ các đường thẳng vuông góc với CM tại H . Cắt AC tại D . Chứng minh tam giác AMC đồng dạng với tam giác HMB
c ) Chứng minh AC . AD= AM . AB
d ) Chứng minh DM vuông góc với BC

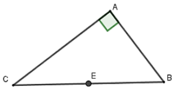
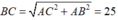 nên bán kính R = 25/2
nên bán kính R = 25/2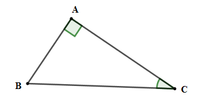
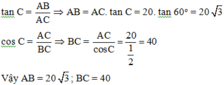


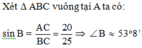

شءشيلبتال
ءبسس
سللباتةتثعي
يسل
a, Áp dụng định lý Py-ta-go vào tam giác ABC vuông tại A , ta có :
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AC^2=BC^2-AB^2\)
\(\Rightarrow AC^2=25^2-20^2\)
\(\Rightarrow AC^2=225\)
\(\Rightarrow AC=15cm\)
Vậy AC = 15cm .
b,Xét tam giác AMC và tam giác HMB có :
góc MAC = góc MHB = 90độ
góc AMC = góc HMB ( đối đỉnh )
Do đó : tam giác AMC đồng dạng với tam giác HMB ( g.g )
c,Xét tam giác ADB và tam giác AMC có :
góc BAD = góc CAM = 90độ
góc ABD = góc ACM ( vì tam giác AMC đồng dạng với tam giác HMB )
Do đó : tam giác ADB đồng dạng với tam giác AMC ( g.g )
\(\Rightarrow\frac{AC}{AB}=\frac{AM}{AD}\)
\(\Rightarrow AC.AD=AM.AB\)
d, Xét tam giác DBC có BA cắt HC tại M :
\(CH\perp BD\)
\(BA\perp DC\)
\(\Rightarrow\)M là trực tâm của tam giác DBC
Vậy DM vuông góc với BC .
Học tốt