Bài 34 (trang 119 SGK Toán 9 Tập 1)
Cho hai đường tròn (O; 20cm) và (O'; 15cm) cắt nhau tại A và B. Tính đoạn nối tâm OO', biết rằng AB = 24 cm. (Xét hai trường hợp: O và O' nằm khác phía đối với AB; O và O' nằm cùng phía đối với AB).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LM
Lê Minh Vũ
VIP
9 tháng 5 2021
Vẽ OM⊥AB⇒OM⊥CD.
Xét đường tròn (O;OC) (đường tròn nhỏ) có OM là một phần đường kính, CD là dây và OM⊥CD nên M là trung điểm của CD hay MC=MD (định lý)
Xét đường tròn (O;OA) (đường tròn lớn) có OM là một phần đường kính, AB là dây và OM⊥AB nên M là trung điểm của AB hay MA=MB (định lý)
Ta có MA=MB và MC=MD (cmt) nên trừ các đoạn thẳng theo vế với vế ta được MA−MC=MB−MD ⇒AC=BD.
Nhận xét. Kết luận bài toán vẫn được giữ nguyên nếu C và D đổi chỗ cho nhau.
T
6 tháng 5 2021
Lời giải:
a) Gọi H là giao điểm của OC và AB, ΔAOB cân tại O (OA = OB, bán kính). OH là đường cao nên cũng là đường phân giác. Do đó:
Suy ra: CB vuông góc với OB, mà OB là bán kính của đường tròn (O)
⇒ CB là tiếp tuến của đường tròn (O) tại B. (điều phải chứng minh)
b) Ta có: OH vuông góc AB nên H là trung điểm của AB (quan hệ vuông góc giữa đường kính và dây)
Vậy OC = 25 cm
LM
Lê Minh Vũ
VIP
9 tháng 5 2021
Vẽ OM⊥AB⇒OM⊥CD.
Xét đường tròn (O;OC) (đường tròn nhỏ) có OM là một phần đường kính, CD là dây và OM⊥CD nên M là trung điểm của CD hay MC=MD (định lý)
Xét đường tròn (O;OA) (đường tròn lớn) có OM là một phần đường kính, AB là dây và OM⊥AB nên M là trung điểm của AB hay MA=MB (định lý)
Ta có MA=MB và MC=MD (cmt) nên trừ các đoạn thẳng theo vế với vế ta được MA−MC=MB−MD ⇒AC=BD.
Nhận xét. Kết luận bài toán vẫn được giữ nguyên nếu C và D đổi chỗ cho nhau.
LM
Lê Minh Vũ
VIP
9 tháng 5 2021
á em lộn
a) Cho hai đường tròn (O; R)(O; R) và (O′; r)(O′; r) với R>r. Nếu OO′=R−rOO′=R−r thì hai đường tròn tiếp xúc trong.
b) +) Nếu tam giác có ba đỉnh nằm trên đường tròn và có 1 cạnh là đường kính của đường tròn đó thì tam giác đó là tam giác vuông.
+) Trong một đường tròn, đường kính vuông góc với dây thì đi qua trung điểm của dây đó.
6 tháng 5 2021
\(=\sqrt{64}=8\left(cm\right)\)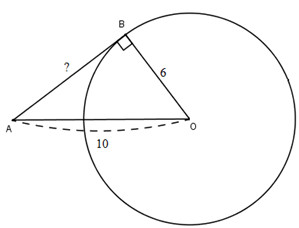
Áp dụng định lý Pytago vào tam giác AOB vuông tại B, ta có:
AB=\(\sqrt{AO^2-OB^2}=\sqrt{10^2-6^2}\)\(=\sqrt{64}=8\left(cm\right)\)
PD
Phạm Đăng Khôi
VIP
25 tháng 7 2021
Câu 3: Tâm của đường tròn ( O) tiếp xúc với 2 cạnh đường Ay , Ax nằm trên đường phân giác OA
30 tháng 4 2021
a) Trong đường tròn nhỏ:
AB > CD => OH < OK (định lí 3)
b) Trong đường tròn lớn:
OH < OK => ME > MF (định lí 3)
c) Trong đường tròn lớn:
ME > MF => MH > MK
DH
30 tháng 4 2021
a) Xét trong đường tròn nhỏ:
Theo định lí : trong hai dây của một đường tròn, dây nào lớn hơn thì dây đó gần tâm hơn.
Theo giả thiết suy ra gần tâm hơn, tức là .
b) Xét trong đường tròn lớn:
Theo định lí : trong hai dây của một đường tròn, dây nào gần tâm hơn thì dây đó lớn hơn.
Theo câu , ta có: .
c) Xét trong đường tròn lớn:
Vì (Định lý 2 - trang 103).
Vì (Định lý 2 - trang 103).
Theo câu , ta có:
- Trường hợp 1: O và O' nằm khác phía đối với AB
Gọi I là giao điểm của OO' và AB. Theo tính chất đường nối tâm ta có:
AB ⊥ OO' và AI = IB = 12
Áp dụng định lí Pitago, ta được:
Vậy OO' = OI + IO' = 16 + 9 = 25 (cm)
- Trường hợp 2: O và O' nằm cùng phía đối với AB
Tương tự như trường hợp 1, ta có:
Vậy OO' = OI – O'I = 16 – 9 = 7 (cm).