Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Trong đường tròn nhỏ:
AB > CD => OH < OK (định lí 3)
b) Trong đường tròn lớn:
OH < OK => ME > MF (định lí 3)
c) Trong đường tròn lớn:
ME > MF => MH > MK

a) Xét đường tròn nhỏ ta được .
b) Xét đường tròn lớn ta được .
c) Từ kết quả câu b) suy ra .

Lời giải chi tiết
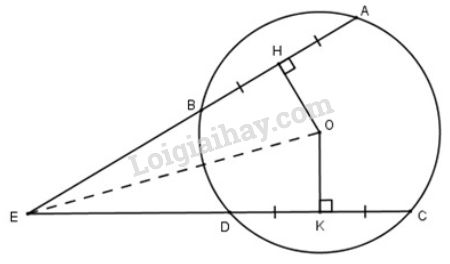
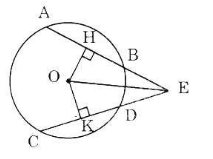
a) Nối OE.
Vì HA=HBHA=HB nên OH⊥ABOH⊥AB (ĐLí 2 - trang 103: đường kính đi qua trung điểm của dây không đi qua tâm thì vuông góc với dây đó)
Vì KC=KDKC=KD nên OK⊥CDOK⊥CD. (ĐLí 2 - trang 103: đường kính đi qua trung điểm của dây không đi qua tâm thì vuông góc với dây đó)
Mặt khác, AB=CDAB=CD nên OH=OKOH=OK (hai dây bằng nhau thì cách đều tâm).
Xét ΔHOEΔHOE và ΔKOEΔKOE có:
OH=OKOH=OK
EOEO chung
ˆEHO=ˆEKO=900EHO^=EKO^=900
Suy ra ΔHOE=ΔKOEΔHOE=ΔKOE (cạnh huyền - cạnh góc vuông)
Suy ra EH=EK(1)EH=EK(1)
b) Theo giả thiết, AB=CDAB=CD nên AB2=CD2AB2=CD2 hay AH=KCAH=KC (2)
Từ (1) và (2) suy ra EH+HA=EK+KCEH+HA=EK+KC
hay EA=EC.
a) Nối OE ta có: AB = CD
=> OH = OK (hai dây bằng nhau thì cách đều tâm)
H là trung điểm của AB nên OH ⊥ AB (đường kính đi qua trung điểm của dây không đi qua tâm thì vuông góc với dây đó)
K là trung điểm của CD nên OK ⊥ CD (đường kính đi qua trung điểm của dây không đi qua tâm thì vuông góc với dây đó)
Hai tam giác vuông OEH và OEK có:
OE là cạnh chung
OH = OK
Do đó ΔOEH = ΔOEK (cạnh huyền, cạnh góc vuông)
=> EH = EK (1). (đpcm)
b) Ta có: H là trung điểm của AB nên AH = \(\frac{1}{2}\)AB
K là trung điểm của CD nên CK = \(\frac{1}{2}\)CD
\(AH=\frac{1}{2}AB\)(định lí 1)
Tương tự ta có KC = \(\frac{1}{2}\)CD
Mà AB = CD (gt) suy ra AH = KC (2)
Từ (1) và (2) suy ra:
EA = EH + HA = EK + KC = EC
Vậy EA = EC. (đpcm)
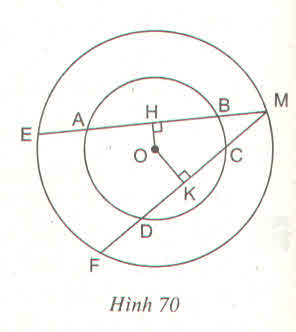
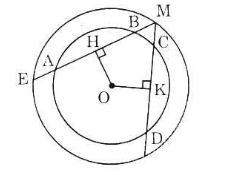

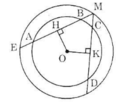
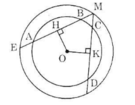
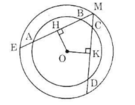
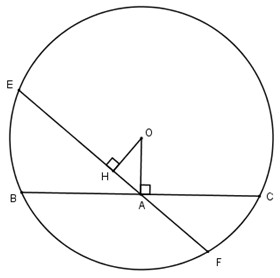
a) Trong đường tròn nhỏ:
AB > CD => OH < OK (định lí 3)
b) Trong đường tròn lớn:
OH < OK => ME > MF (định lí 3)
c) Trong đường tròn lớn:
ME > MF => MH > MK
a) Xét trong đường tròn nhỏ:
Theo định lí 22: trong hai dây của một đường tròn, dây nào lớn hơn thì dây đó gần tâm hơn.
Theo giả thiết AB>CDAB>CD suy ra ABAB gần tâm hơn, tức là OH<OKOH<OK.
b) Xét trong đường tròn lớn:
Theo định lí 22: trong hai dây của một đường tròn, dây nào gần tâm hơn thì dây đó lớn hơn.
Theo câu aa, ta có: OH<OK⇒ME>MFOH<OK⇒ME>MF.
c) Xét trong đường tròn lớn:
Vì OH⊥ME⇒EH=MH=ME2OH⊥ME⇒EH=MH=ME2 (Định lý 2 - trang 103).
Vì OK⊥MF⇒KF=MK=MF2OK⊥MF⇒KF=MK=MF2 (Định lý 2 - trang 103).
Theo câu bb, ta có: ME>MF⇒ME2>MF2⇔MH>MK