1Tìm m để phương trình mcos²x - msin2x - msin²x=0 để phương trình có nghiệm.
2 Tìm x € (0; π/2) thỏa mãn pt cos5x.sin4x = cos3x.sin2x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 1 2017
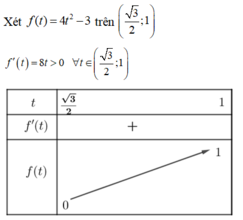
Dựa vào bảng biến thiên phương trình có nghiệm khi 0<m<1
Chọn D
CM
23 tháng 5 2017
Đáp án C
Ta có
f ' x = − m s i n x + 2 cos x − 3 ; y ' = 0 ⇔ − m s i n x + 2 cos x = 3
Phương trình này giải được với điều kiện là
m 2 + 2 2 ≥ 3 2 ⇔ m 2 ≥ 5 ⇔ m ∈ − ∞ ; − 5 ∪ 5 ; + ∞
CM
24 tháng 6 2017
Đáp án C
Ta có: cos 2 3 x 1 + cos 6 x 2 = 4 cos 3 2 x − 3 cos 2 x + 1 2 và cos 4 x = 2 cos 2 2 x − 1
Khi đó, phương trình đã cho
⇔ 2 cos 2 2 x − 1 = 4 cos 3 2 x − 3 cos 2 x + 1 2 + 1 − cos 2 x 2 m
⇔ 4 cos 2 2 x − 2 = 4 cos 3 2 x − 3 cos 2 x + 1 + 1 − cos 2 x m
⇔ cos 2 x − 1 m = 4 cos 3 2 x − 4 cos 2 2 x − 3 cos 2 x + 3
Đặt t = cos 2 x , với x ∈ 0 ; π 12 → t ∈ 3 2 ; 1 do đó: * ⇔ m 4 t 3 − 4 t 2 − 3 t + 3 t − 1 = 4 t 2 − 3
Xét hàm số f t = 4 t 2 − 3 trên khoảng 3 2 ; 1 → min f t = 0 max f t = 1
Vậy để phương trình m = f t có nghiệm khi và chỉ khi m ∈ 0 ; 1
, do đó (*) 
CM
12 tháng 5 2018
Đáp án C
Ta có c os 2 3 x = 1 + c os 6 x 2 = 4 c os 3 2 x − 3 c os 2 x + 1 2
và c os 4 x = 2 c os 2 2 x − 1
Khi đó, phương trình đã cho
⇔ 2 c os 2 2 x − 1 = 4 c os 3 2 x − 3 c os 2 x + 1 2 + 1 − c os 2 x 2 m
⇔ 4 c os 2 2 x − 2 = 4 c os 3 2 x − 3 c os 2 x + 1 + 1 − c os 2 x m ⇔ c os 2 x − 1 m = 4 c os 3 2 x − 4 c os 2 2 x − 3 c os 2 x + 3
Đặt t = c os 2 x , với x ∈ 0 ; π 12 → t ∈ 3 2 ; 1 ,
do đó (*) ⇔ m = 4 t 3 − 4 t 2 − 3 t + 3 t − 1 = 4 t 2 − 3.
Xét hàm số f t = 4 t 2 − 3 trên khoảng 3 2 ; 1 → min f t = 0 max f t = 1 .
Vậy để phương trình m = f t có nghiệm khi và chỉ khi m ∈ 0 ; 1 .
HP
13 tháng 8 2021
1.
a, Phương trình có nghiệm khi:
\(\left(m+2\right)^2+m^2\ge4\)
\(\Leftrightarrow m^2+4m+4+m^2\ge4\)
\(\Leftrightarrow2m^2+4m\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}m\ge0\\m\le-2\end{matrix}\right.\)
b, Phương trình có nghiệm khi:
\(m^2+\left(m-1\right)^2\ge\left(2m+1\right)^2\)
\(\Leftrightarrow2m^2+6m\le0\)
\(\Leftrightarrow-3\le m\le0\)
HP
13 tháng 8 2021
2.
a, Phương trình vô nghiệm khi:
\(\left(2m-1\right)^2+\left(m-1\right)^2< \left(m-3\right)^2\)
\(\Leftrightarrow4m^2-4m+1+m^2-2m+1< m^2-6m+9\)
\(\Leftrightarrow4m^2-7< 0\)
\(\Leftrightarrow-\dfrac{\sqrt{7}}{2}< m< \dfrac{\sqrt{7}}{2}\)
b, \(2sinx+cosx=m\left(sinx-2cosx+3\right)\)
\(\Leftrightarrow\left(m-2\right)sinx-\left(2m+1\right)cosx=-3m\)
Phương trình vô nghiệm khi:
\(\left(m-2\right)^2+\left(2m+1\right)^2< 9m^2\)
\(\Leftrightarrow m^2-4m+4+4m^2+4m+1< 9m^2\)
\(\Leftrightarrow m^2-1>0\)
\(\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\)
CM
9 tháng 12 2018
Đáp án B
PT
Đặt
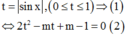
Để (1) có nghiệm thì (2) có nghiệm 
có nghiệm 
Suy ra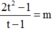 
có nghiệm 
Xét hàm số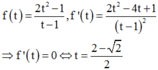 
Lập bảng biến thiên hàm số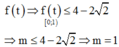 
CM
15 tháng 8 2018
Đáp án B
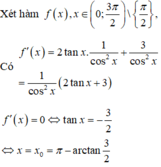
Bảng biến thiên
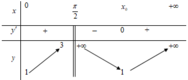
Từ BBt ta thấy, để phương trình có 3 nghiệm phân biệt trong khoảng
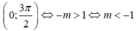
Cách 2 (casio): Thử bằng MTCT, sử dụng Mode 7
+ Thử với m = -2 ta thấy f(x) đổi dấu 3 lần nên có 3 nghiệm (loại đáp án C,D)
+ Thử với m = -1 ta thấy f(x) đổi dấu 2 lần nên có 2 nghiệm (loại A).
1,
Nếu m = 0, phương trình có tập nghiệm là S = R, thỏa mãn yêu cầu bài toán
Nếu m ≠ 0 phương trình tương đương
cos2x - sin2x - sin2x = 0 ⇔ cos2x = sin2x, luôn có nghiệm trên R
Vậy m nào cũng sẽ thỏa mãn ycbt