
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a. Trừ vế theo vế \(\left(1\right)\) cho \(\left(2\right)\) ta được \(x^2-y^2=4x-4y\)
\(\Leftrightarrow\left(x-y\right)\left(x+y-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=y\\x=4-y\end{matrix}\right.\)
TH1: \(x=y\)
Phương trình \(\left(1\right)\) tương đương:
\(x^2=2x\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=y=0\\x=y=2\end{matrix}\right.\)
TH2: \(x=4-y\)
Phương trình \(\left(2\right)\) tương đương:
\(y^2=4y-4\)
\(\Leftrightarrow y^2-4y+4=0\)
\(\Leftrightarrow\left(y-2\right)^2=0\)
\(\Leftrightarrow y=2\)
\(\Rightarrow x=2\)
Vậy hệ đã cho có nghiệm \(\left(x;y\right)\in\left\{\left(0;0\right);\left(2;2\right)\right\}\)
b. \(\left\{{}\begin{matrix}x+y+xy=5\\x^2+y^2=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy=5-\left(x+y\right)\\\left(x+y\right)^2-2xy=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy=5-\left(x+y\right)\\\left(x+y\right)^2-10+2\left(x+y\right)=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy=5-\left(x+y\right)\\\left(x+y\right)^2+2\left(x+y\right)-15=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy=5-\left(x+y\right)\\\left(x+y+5\right)\left(x+y-3\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy=5-\left(x+y\right)\\\left[{}\begin{matrix}x+y=-5\\x+y=3\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x+y=-5\\xy=10\end{matrix}\right.\\\left\{{}\begin{matrix}x+y=3\\xy=2\end{matrix}\right.\end{matrix}\right.\)
TH1: \(\left\{{}\begin{matrix}x+y=-5\\xy=10\end{matrix}\right.\Leftrightarrow\) vô nghiệm
TH2: \(\left\{{}\begin{matrix}x+y=3\\xy=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\\\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\end{matrix}\right.\)
Vậy ...

Trừ vế cho vế phương trình (1) cho (2) ta được:
x 2 + y 2 − y = − 1 ⇔ x 2 + y 2 − y + 1 = 0
Ta có:
x 2 ≥ 0 , ∀ x y 2 − y + 1 = y − 1 2 2 + 3 4 > 0 , ∀ y ⇒ x 2 + y 2 − y + 1 > 0 , ∀ x , y
Do đó phương trình x 2 + y 2 − y + 1 = 0 vô nghiệm
Vậy không tồn tại giá trị của xy
Đáp án cần chọn là: D

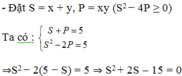
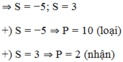
Khi đó: x, y là nghiệm của phương trình X 2 - 3 X + 2 = 0 ⇔ X = 1 ; X = 2
Vậy hệ có nghiệm (2; 1), (1; 2)
Đáp án cần chọn là: C




ĐKXĐ : \(x;y\ne0\)
Ta có \(\dfrac{y}{x}-\dfrac{2x}{y}=\dfrac{-5}{2}-\dfrac{2}{xy}\)
\(\Leftrightarrow\dfrac{y^2-2x^2}{xy}=\dfrac{-5xy-4}{2xy}\)
\(\Leftrightarrow2y^2-4x^2+5xy=-4\) (1)
Kết hợp \(x^2+xy-y^2=5\) (2)
ta có : \(-5.\left(2y^2-4x^2+5xy\right)=4\left(x^2+xy-y^2\right)\)
\(\Leftrightarrow16x^2-29xy-6y^2=0\)
\(\Leftrightarrow16x^2-32xy+3xy-6y^2=0\)
\(\Leftrightarrow\left(x-2y\right)\left(16x+3y\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2y\\x=-\dfrac{3y}{16}\end{matrix}\right.\)
Thay \(x=-\dfrac{3y}{16}\) vào (2) ta được
\(\dfrac{9y^2}{256}-\dfrac{3y^2}{16}-y^2=5\)
\(\Leftrightarrow y^2=-\dfrac{256}{59}\Leftrightarrow y\in\varnothing\) (loại)
Khi x = 2y thay vào (2) ta được
4y2 + 2y2 - y2 = 5
\(\Leftrightarrow y=\pm1\) (tm)
Với y = 1 => x = 2
y = -1 => x = -2
Vậy (x;y) = (2;1) ; (-2;-1)
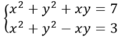
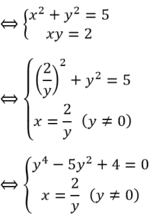

Ta có hệ phương trình : \(\left\{{}\begin{matrix}x+xy+y=5\\x^2+y^2=5\left(I\right)\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x+y=5-xy\\x^2+y^2+2xy=5+2xy\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x+y=5-xy\\\left(x+y\right)^2=5+2xy\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x+y=5-xy\\\left(5-xy\right)^2=5+2xy\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x+y=5-xy\\25-10xy+x^2y^2-5-2xy=0\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x+y=5-xy\\20-12xy+x^2y^2=0\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x+y=5-xy\\\left(xy\right)^2-2xy-10xy+20=0\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x+y=5-xy\\\left(xy-10\right)\left(xy-2\right)=0\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x+y=5-xy\\\left[{}\begin{matrix}xy-10=0\\xy-2=0\end{matrix}\right.\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}x+y=5-xy\\\left[{}\begin{matrix}x=10\\x=2\end{matrix}\right.\end{matrix}\right.\)
TH1 : x = 10 .
- Thay x = 10 vào phương trình ( I ) ta được :
\(10^2+y^2=5\)
=> \(y^2=-95\) ( vô lý )
-> x = 10 ( loại )
TH2 : x = 2 .
- Thay x = 2 vào phương trình ( I ) ta được :
\(2^2+y^2=5\)
=> \(y^2=1\)
=> \(y=1\)
Vậy phương trình trên có nghiệm duy nhất là \(\left(x;y\right)=\left(2;1\right)\)