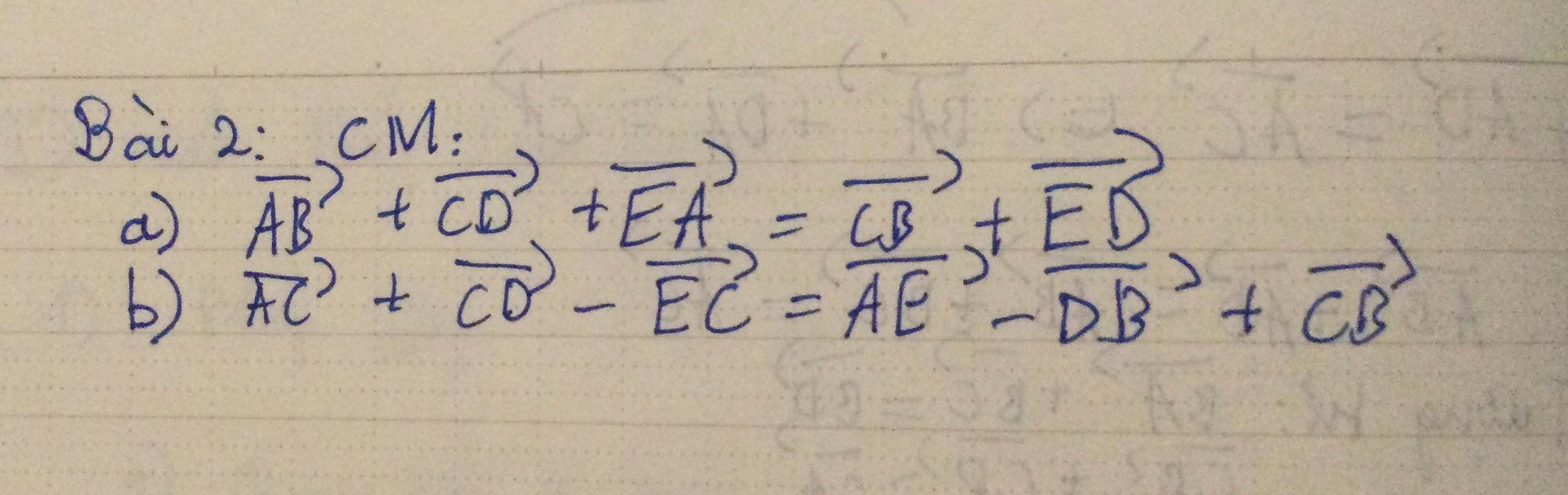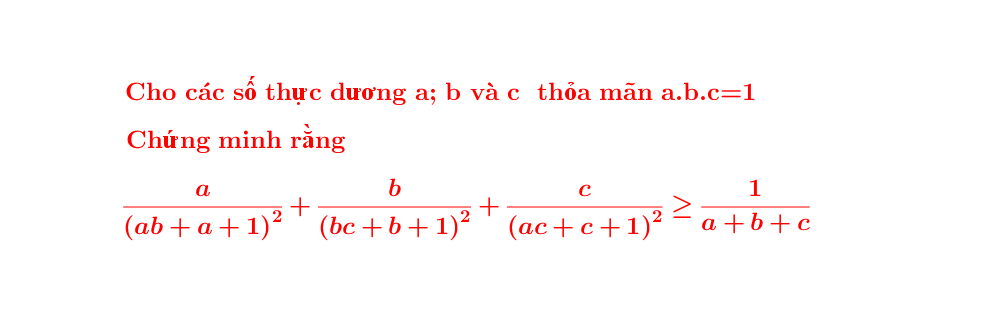K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PK
0
NM
2
HP
3 tháng 9 2021
b, \(\vec{AC}+\vec{CD}-\vec{EC}\)
\(=\vec{AE}+\vec{EC}+\vec{BD}-\vec{BC}-\vec{EC}\)
\(=\vec{AE}-\vec{DB}+\vec{CB}\)
PK
0
PK
0
NM
10
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 4 2022
\(\dfrac{ab}{a+3b+2c}=\dfrac{ab}{\left(a+c\right)+\left(b+c\right)+2b}\le\dfrac{1}{9}\left(\dfrac{ab}{a+c}+\dfrac{ab}{b+c}+\dfrac{ab}{2b}\right)\)
\(=\dfrac{1}{9}\left(\dfrac{ab}{a+c}+\dfrac{ab}{b+c}+\dfrac{a}{2}\right)\)
Tương tự:
\(\dfrac{bc}{b+3c+2a}\le\dfrac{1}{9}\left(\dfrac{bc}{a+b}+\dfrac{bc}{a+c}+\dfrac{b}{2}\right)\)
\(\dfrac{ac}{c+3a+2b}\le\dfrac{1}{9}\left(\dfrac{ac}{b+c}+\dfrac{ac}{a+b}+\dfrac{c}{2}\right)\)
Cộng vế:
\(P\le\dfrac{1}{9}\left(\dfrac{bc+ac}{a+b}+\dfrac{bc+ab}{a+c}+\dfrac{ab+ac}{b+c}+\dfrac{a+b+c}{2}\right)\)
\(P\le\dfrac{1}{9}.\left(a+b+c+\dfrac{a+b+c}{2}\right)=\dfrac{1}{2}\)
Dấu "=" xảy ra khi \(a=b=c=1\)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 2 2022
\(VT=\sqrt{\left(a+\dfrac{5b}{2}\right)^2+\dfrac{15b^2}{4}}+\sqrt{\left(b+\dfrac{5c}{2}\right)^2+\dfrac{15c^2}{4}}+\sqrt{\left(c+\dfrac{5a}{2}\right)^2+\dfrac{15a^2}{4}}\)
\(\Rightarrow VT\ge\sqrt{\left(a+\dfrac{5b}{2}+b+\dfrac{5c}{2}+c+\dfrac{5a}{2}\right)^2+\dfrac{15}{4}\left(a+b+c\right)^2}\)
\(\Rightarrow VT\ge\sqrt{\dfrac{49}{4}\left(a+b+c\right)^2+\dfrac{15}{4}\left(a+b+c\right)^2}=4\left(a+b+c\right)\)
Dấu "=" xảy ra khi \(a=b=c\)
