
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hai đường thẳng cắt nhau và không cùng nằm trong một mặt phẳng : AB và C C 1 ; A A 1 và CD; ...

Đường thẳng nằm trong mặt phẳng: AB nằm trong mp( A B B 1 A 1 ); AB và mp(ABCD); .

Đường thẳng không có điểm chung với mặt phẳng : AB và mp( C D D 1 C 1 ); AB và mp ( A 1 B 1 C 1 D 1 ); ...

Đường thẳng cắt mặt phẳng : A A 1 cắt mp (ABCD) tại A; A A 1 cắt mp ( A 1 B 1 C 1 D 1 ) tại A 1 ; ...

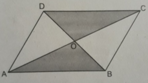
Xem hình bs.52.
- Các tam giác ADB, ACB, DAC, DBC có diện tích bằng nhau vì cùng bằng nửa diện tích hình bình hành đã cho.
- Các tam giác OAD, OCB, ODC, OBA có diện tích bằng nhau vì cùng bằng một phần tư diện tích hình bình hành đã cho.

Ta có:
* SADB=SACB=SDAC=SDBC ( cùng bằng \(\dfrac{1}{2}.S_{hbh}\) )
* SOAD=SOCB=SODC=SOBA (cùng bằng \(\dfrac{1}{4}.S_{hbh}\))

a, Ta có: BE song song AC ( theo bài ra)
AB song song CE ( E thuộc CD)
nên ABEC là hình bình hành, do đó AC=BE
mà AC = BD
nên BD=BE do đó BDE là tam giác cân
b, Ta có AC song song BE nên ˆBEC=ˆACD
mà ˆBED=ˆBDC ( BDE là tam giác cân )
do đó ˆACD=ˆBDC
Xét tg ACD và tg BDC có : ˆACD=ˆBDC
AC=BD( theo gt )
BC là cạnh chung
nên tg ACD =tg BDC ( c-g-c)
c, Theo chứng minh câu b, ta có: tg ACD= tg BDC
do đó ˆADC=ˆBCD
Vậy ABCD là hình thang cân
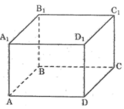
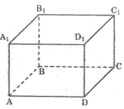
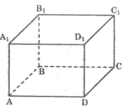
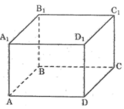
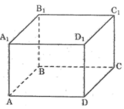
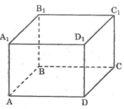
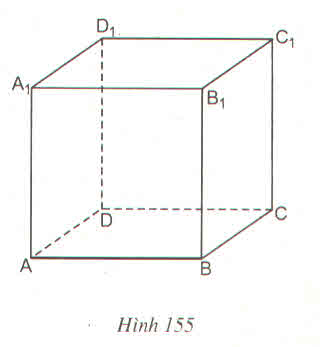


Hai đường thẳng cắt nhau: AD và DC; AD và D D 1 ; B B 1 và BC; ...