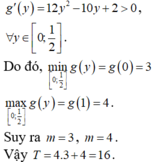Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì \(x\ge1\Rightarrow x^2\ge x\)
Từ đó: \(P\ge\frac{x}{\left(x+y\right)^2+x}+\frac{x}{z^2+x}=x\left[\frac{1}{\left(x+y\right)^2+x}+\frac{1}{z^2+x}\right]\)
\(\ge x\cdot\frac{4}{\left(x+y\right)^2+x+z^2+x}=\frac{4x}{\left(x+y\right)^2+z^2+2x}\) (Cauchy Schwarz)
Lại có: \(\left(x+y\right)^2+z^2=x^2+y^2+z^2+2xy=3\left(x+y+z\right)\)
\(\le3\sqrt{2\left[\left(x+y\right)^2+z^2\right]}\)
\(\Rightarrow\left(x+y\right)^2+z^2\le18\)
\(\Rightarrow P\ge\frac{4x}{18+2x}=2-\frac{18}{x+9}\ge2-\frac{18}{1+9}=\frac{1}{5}\)
Dấu "=" xảy ra khi: \(\hept{\begin{cases}x=1\\y=2\\z=3\end{cases}}\)
Vậy Min(P) = 1/5 khi x = 1 ; y = 2 ; z = 3

Áp dụng BĐT Cô-si ta có:
\(1+x^3+y^3\ge3\sqrt[3]{1.x^3.y^3}=3xy\Rightarrow\sqrt{1+x^3+y^3}\ge\sqrt{3xy}\Rightarrow\frac{\sqrt{1+x^3+y^3}}{xy}\ge\frac{\sqrt{3xy}}{xy}\)
Tương tự:\(\frac{\sqrt{1+y^3+z^3}}{yz}\ge\frac{\sqrt{3yz}}{yz};\frac{\sqrt{1+z^3+x^3}}{zx}\ge\frac{\sqrt{3zx}}{zx}\)
Công vế với vế của 3 BĐT trên ta đươc:
\(P\ge\frac{\sqrt{3xy}}{xy}+\frac{\sqrt{3yz}}{yz}+\frac{\sqrt{3zx}}{zx}=\sqrt{3}\left(\frac{1}{\sqrt{xy}}+\frac{1}{\sqrt{yz}}+\frac{1}{\sqrt{zx}}\right)\) \(=\sqrt{3}.\left(\sqrt{x}+\sqrt{y}+\sqrt{z}\right)\ge3\sqrt{3}\)
Dấu '='xảy ra khi \(\hept{\begin{cases}x=y=z\\xyz=1\end{cases}\Leftrightarrow x=y=z=1}\)
Vậy \(P_{min}=3\sqrt{3}\)khi \(x=y=z=1\)
:))