Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Ta có m a x [ 1 ; 2 ] y + m i n [ 1 ; 2 ] y = y ( 1 ) + y 2 = m + 1 2 + m + 2 3 = 16 3 ⇒ 5 m + 7 6 = 16 3
⇔
5
m
+
7
=
32
⇒
m
=
5

Đáp án A
ln 1 - 2 x x + y = 3 x + y - 1 , 0 < x < 1 2 , y > 0 ⇔ ln 1 - 2 x + 1 - 2 x = ln ( x + y ) + x + y f t = t + ln t ⇒ f ' t = 1 + 1 t > 0 ⇒ f 1 - 2 x = f ( x + y ) ⇔ 1 - 2 x = x + y ⇔ y = 1 - 3 x P = 1 x + 1 x y = 1 x + 1 x 1 - 3 x ⇒ P ' = - 1 x 2 + 6 x - 1 2 x 1 - 3 x x ( 1 - 3 x ) = - 2 x 1 - 3 x ( 1 - 3 x ) + ( 6 x - 1 ) x 2 x 1 - 3 x x 2 ( 1 - 3 x ) P ' = 0 ⇔ 2 x 1 - 3 x ( 1 - 3 x ) = 6 x 2 - x ⇔ 6 x 2 - x > 0 4 x ( 1 - 3 x ) 3 = 6 x 2 - x 2 ⇔ [ x < 0 x > 1 6 4 x - 36 x 2 + 108 x 3 - 108 x 4 = 26 x 4 - 12 x 3 + x 2 ⇔ x = y = 1 4 ⇒ P = 8

Đáp án C.
Ta có
1 = x + y ≥ 2 x y ⇒ x y ≤ 1 2 ⇒ 0 ≤ x y ≤ 1 4
⇒ P = x 2 + x + y 2 + y x y + x + y + 1 = x + y 2 − 2 x y + 1 x y + 1 + 1 = 2 − 2 x y x y + 2
Đặt t = x y ⇒ t ∈ 0 ; 1 4 ⇒ P = 2 − 2 t t + 2 = f t
Bảng biến thiên:
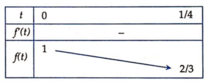
=> M + m = 5 3

ĐK:
![]()
Ta có
log 3 1 - y x + 3 x y = 3 x y + x + 3 y - 4
![]()
![]()
![]()

Xét hàm số f ( x ) = log 3 t + 3 t t > 0
có f ' ( t ) = 1 t ln 3 + 3 > 0 ; ∀ t > 0 nên hàm số đồng biến trên 0 ; + ∞
Kết hợp (*) suy ra
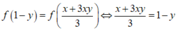
![]()
Xét P = x + y ⇒ x = P - y thay vào (**) ta được
![]()
![]()
Ta tìm giá trị nhỏ nhất của g ( y ) = 3 y 2 - 2 y + 3 3 y + 1 trên (0;1)
Ta có
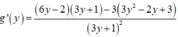
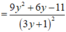
Giải phương trình
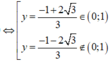
Lại có g ' ( y ) < 0 ∀ y ∈ 0 ; - 1 + 2 3 3
và g ' ( y ) > 0 ∀ y ∈ - 1 + 2 3 3 ; 1
Hay g'(y) đổi dấu từ âm sang dương tại y = - 1 + 2 3 3 nên
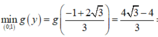
⇒ P m i n = 4 3 - 4 3
Chọn đáp án A.

Đáp án B.
Từ giả thiết, suy ra 5 x + 2 y + 1 3 x y - 1 + x + 1 = 5 x y - 1 + 1 3 x + 2 y + x y - 2 y
⇔ 5 x + 2 y - 1 3 x + 2 y + x + 2 y = 5 x y - 1 - 1 3 x y - 1 + ( x y - 1 ) (1)
Xét hàm số f ( t ) = 5 t - 1 3 t + t trên ℝ .
Đạo hàm f ' ( t ) = 5 t . ln 5 + ln 3 3 t + 1 > 0 , ∀ t ∈ ℝ ⇒ hàm số f (t) luôn đồng biến trên ℝ .
Suy ra 1 ⇔ f ( x + 2 y ) = f ( x y - 1 ) ⇔ x + 2 y = x y - 1 ⇔ x + 1 = y ( x - 2 )
y = x + 1 x - 2
Do y > 0 nên x + 1 x - 2 > 0 ⇔ x > 2 x < - 1 . Mà x > 0 nên x > 2.
Từ đó T = x + y = x + x + 1 x - 2 . Xét hàm số g ( x ) = x + x + 1 x - 2 trên 2 ; + ∞ .
Đạo hàm g ' ( x ) = 1 - 3 x - 2 2 > 0 , g ' ( x ) = 0 ⇔ ( x - 2 ) 2 = 3
⇔ x = 2 + 3 ( t m ) x = 2 - 3 ( L ) . Lập bảng biến thiên của hàm số trên 2 ; + ∞ , ta thấy m i n g ( x ) = g ( 2 + 3 ) = 3 + 2 3 .
Vậy T m i n = 3 + 2 3 khi x = 2 + 3 và y = 1 + 3 .
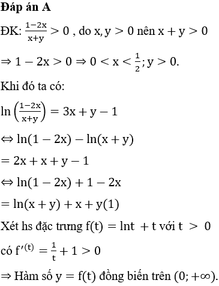






Đáp án A
ln ( 1 − 2 x x + y ) = 3 x + y − 1 , ( 0 < x < 1 2 , y > 0 ) ⇔ ln ( 1 − 2 x ) + 1 − 2 x = ln ( x + y ) + x + y f ( t ) = t + ln t ⇒ f ' ( t ) = 1 + 1 t > 0 ⇒ f ( 1 − 2 x ) = f ( x + y ) ⇔ 1 − 2 x = x + y ⇔ y = 1 − 3 x