Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì (P) đi qua M(4;3) nên 3= 16a+ 4b+c (1)
Mặt khác (P) cắt Ox tại N(3;0) suy ra 0=9a+3b+c (2) , (P) cắt Ox tại P nên P(t; 0) với 0= at2+ bt+c (*) ; (P) cắt Ox tại N và P nên phương trình (*) có 1 nghiệm là t=3 ( hoành độ điểm N)

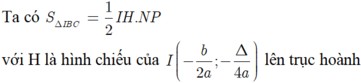
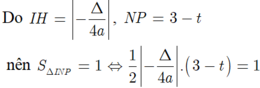
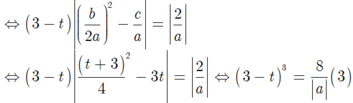
Từ (1) và (2); vế trừ vế ta có 7a+ b=3 hay b= 3-7a
suy ra: 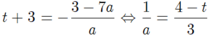
Thay vào (3) ta có:
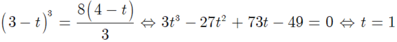
Suy ra a= 1; b= -4; c=3.
Vậy (P) cần tìm là y= x2-4x+3.
Chọn B.

a) Vì parabol đi qua M(1; 5) nên tọa độ của M nghiệm đúng phương trình của parabol: 5 = a.12 + b.1 + 2.
Tương tự, với N(- 2; 8) ta có: 8 = a.(- 2)2 + b.(- 2) + 2
Giải hệ phương trình: ta được a = 2, b = 1.
Parabol có phương trình là: y = 2x2 + x + 2.
b) Giải hệ phương trình:
Parabol: y = x2 - x + 2.
c) Giải hệ phương trình:
Parabol: y = x2 - 4x + 2.
d) Ta có:
Parabol: y = 16x2 + 12x + 2 hoặc y = x2 - 3x + 2.

Hàm số đi qua \(A\left(8;0\right)\) nên: \(a.8^2+8b+c=0\)\(\Leftrightarrow64a+8b+c=0\).
Hàm số có đỉnh là: \(I\left(6;-12\right)\) nên: \(\left\{{}\begin{matrix}\dfrac{-b}{2a}=6\\6^2.a+6b+c=-12\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}12a+b=0\\36a+6b+c=-12\end{matrix}\right.\).
Vậy ta có hệ: \(\left\{{}\begin{matrix}64a+8b+c=0\\-b=12a\\36a+6b+c=-12\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=-36\\c=96\end{matrix}\right.\).
Vậy : \(y=-3x^2-36x+96\).

a)
y(1) =a-4+c=\(-2\)\(\Rightarrow\) a+c=2
y(2)=4a-8+c=3 \(\Rightarrow\)4a+c=3
Trừ cho nhau\(\Rightarrow\)3a=1 \(\Rightarrow\)a=\(\dfrac{1}{3}\)\(\Rightarrow\) \(c=2-\dfrac{1}{3}=\dfrac{5}{3}\).
Vậy: \(y=\dfrac{1}{3}x^2-4x+\dfrac{5}{3}\).
b)
I(-2;1)\(\Rightarrow\dfrac{4}{2a}=-2\)\(\Leftrightarrow a=-1\).
y(-2) \(=-4+8+c=1\)\(\Rightarrow\) \(c=-3\)
Vậy: \(y=-x^2-4x-3\).
c)\(\dfrac{4}{2a}=-3\)\(\Leftrightarrow a=-\dfrac{2}{3}\)
\(y\left(-2\right)=-\dfrac{2}{3}.4+8+c=1\)\(\Leftrightarrow c=-\dfrac{13}{3}\)
Vậy: \(y=-\dfrac{2}{3}x^3-4x-\dfrac{13}{3}\).

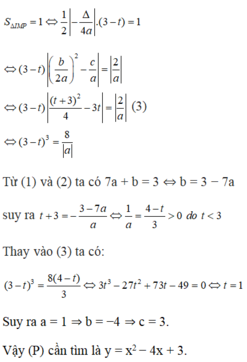
Do (P) đi qua \(M\left(4;3\right)\Rightarrow16a+4b+c=3\)
Do (P) cắt Ox tại \(N\left(3;0\right)\Rightarrow9a+3b+c=0\)
\(\Rightarrow7a+b=3\Rightarrow b=3-7a\)
\(9a+3\left(3-7a\right)+c=0\Rightarrow c=12a-9\)
Phương trình hoành độ giao điểm (P) và Ox: \(ax^2+bx+c=0\)
\(\Delta=b^2-4ac=\left(3-7a\right)^2-4a\left(12a-9\right)=\left(a-3\right)^2\)
Do \(\left\{{}\begin{matrix}x_P< x_I< x_N< x_M\\y_N< y_M\end{matrix}\right.\) \(\Rightarrow\) hàm \(y=ax^2+bx+c\) đồng biến trên \(\left(-\frac{b}{2a};+\infty\right)\)
\(\Rightarrow a>0\)
\(\Rightarrow x_N=\frac{-b+\left|a-3\right|}{2a}=\frac{7a-3+\left|a-3\right|}{2a}=3\)
\(\Rightarrow\left|a-3\right|=3-a\Rightarrow0< a< 3\)
\(\Rightarrow S_{INP}=\frac{1}{2}\left(x_N-x_P\right).\left|\frac{-\Delta}{4a}\right|=\frac{1}{2}\frac{\sqrt{\Delta}}{a}.\frac{\Delta}{4a}=1\)
\(\Leftrightarrow\left(3-a\right)\left(a-3\right)^2=8a^2\)
\(\Leftrightarrow a^3-a^2+27a-27=0\)
\(\Leftrightarrow\left(a-1\right)\left(a^2+27\right)=0\Rightarrow a=1\)
\(\Rightarrow b=-4\) ; \(c=3\)
\(\left(P\right):y=x^2-4x+3\)
Ý bạn là công thức tính diện tích tam giác INP?
Kẻ \(IH\perp Ox\Rightarrow IH=\left|y_I\right|=\left|\frac{-\Delta}{4a}\right|\)
\(NP=\left|x_N-x_P\right|=x_N-x_P=\frac{\sqrt{\Delta}}{a}\) \(\left(\frac{-b+\sqrt{\Delta}}{2a}-\frac{-b-\sqrt{\Delta}}{2a}=\frac{\sqrt{\Delta}}{a}\right)\)
Sau đó thay vào thôi