Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

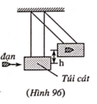
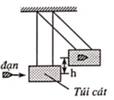
Gọi độ lệch của đầu đạn so với điểm bắn là d
TH1:
Ta cần tìm góc lệch \(\alpha\) của đạn khi có gió thổi.
Tốc độ tổng hợp của đạn: \(v^2=v_{đạn}^2+v_{gió}^2+2.v_{đạn}v_{gió}.\cos{60^0}=832\)(m/s)
Áp dụng hs sin trong tam giác ta có: \(\dfrac{4}{\sin\alpha}=\dfrac{832}{\sin120^0}\Rightarrow\sin\alpha=\dfrac{2\sqrt 3}{832}\)
Suy ra \(\tan\alpha=4,16.10^{-3}\)
Mà \(\tan\alpha=\dfrac{d}{L}\Rightarrow d = \tan\alpha.L=4,16.10^{-3}.500=2,1(m)\)
TH2: Làm tương tự, nhưng dễ hơn vì hướng gió lệch 900
Lúc này: \(\tan\alpha=\dfrac{4}{830}\)
Suy ra góc lệch: \(d=\dfrac{4}{830}.500=2,4(m)\)

Chọn C.
Chọn hệ trục Ox như hình vẽ
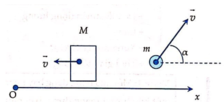
Phương trình bảo toàn véc tơ động lượng cho hệ theo Ox
![]()
Vì trước khi bắn hệ đứng yên
Chiếu phương trình (*) lên Ox ta được: 0 = -p’1 + p’2.cos60o
Thay số ta được:
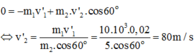

Chọn C.
Chọn hệ trục Ox như hình vẽ
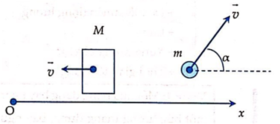
Phương trình bảo toàn véc tơ động lượng cho hệ theo Ox


a. Áp dụng định luật bảo toàn cơ năng xác định được vận tốc của hệ ngay sau khi va chạm là . Từ đó áp dụng định luật bảo toàn động lượng xác định được vận tốc của đạn (lúc đầu vận tốc của túi cát là 0), tức là
, từ đó suy ra v.
b. Áp dụng định luật bảo toàn năng lượng suy ra lượng năng lượng đã chuyển hóa thành nhiệt năng là bằng hiệu cơ năng của hệ lúc đầu và lúc sau, tức là

+ Theo định luật bảo toàn động lượng:
− m 1 + m 2 + m 3 v 1 = m 1 + m 2 v / + m 3 v 0 − v 1
⇒ v / = − m 1 + m 2 + m 3 v 1 − m 3 v 0 − v 1 m 1 + m 2 = − 130 + 20 + 1 .5 − 1 400 − 5 130 + 20 ≈ − 7 , 67 m / s
+ Vận tốc của toa vẫn theo chiều cũ và tăng tốc.
Chọn đáp án B

+ Theo định luật bảo toàn động lượng:
m 1 + m 2 + m 3 v 1 = m 1 + m 2 v / + m 3 v 0 + v 1
⇒ v / = m 1 + m 2 + m 3 v 1 − m 3 v 0 + v 1 m 1 + m 2 = 130 + 20 + 1 .5 − 1 400 + 5 130 + 20 ≈ 2 , 33 m / s
+ Toa xe chuyển động theo chiều bắn nhưng vận tốc giảm đi
Chọn đáp án D