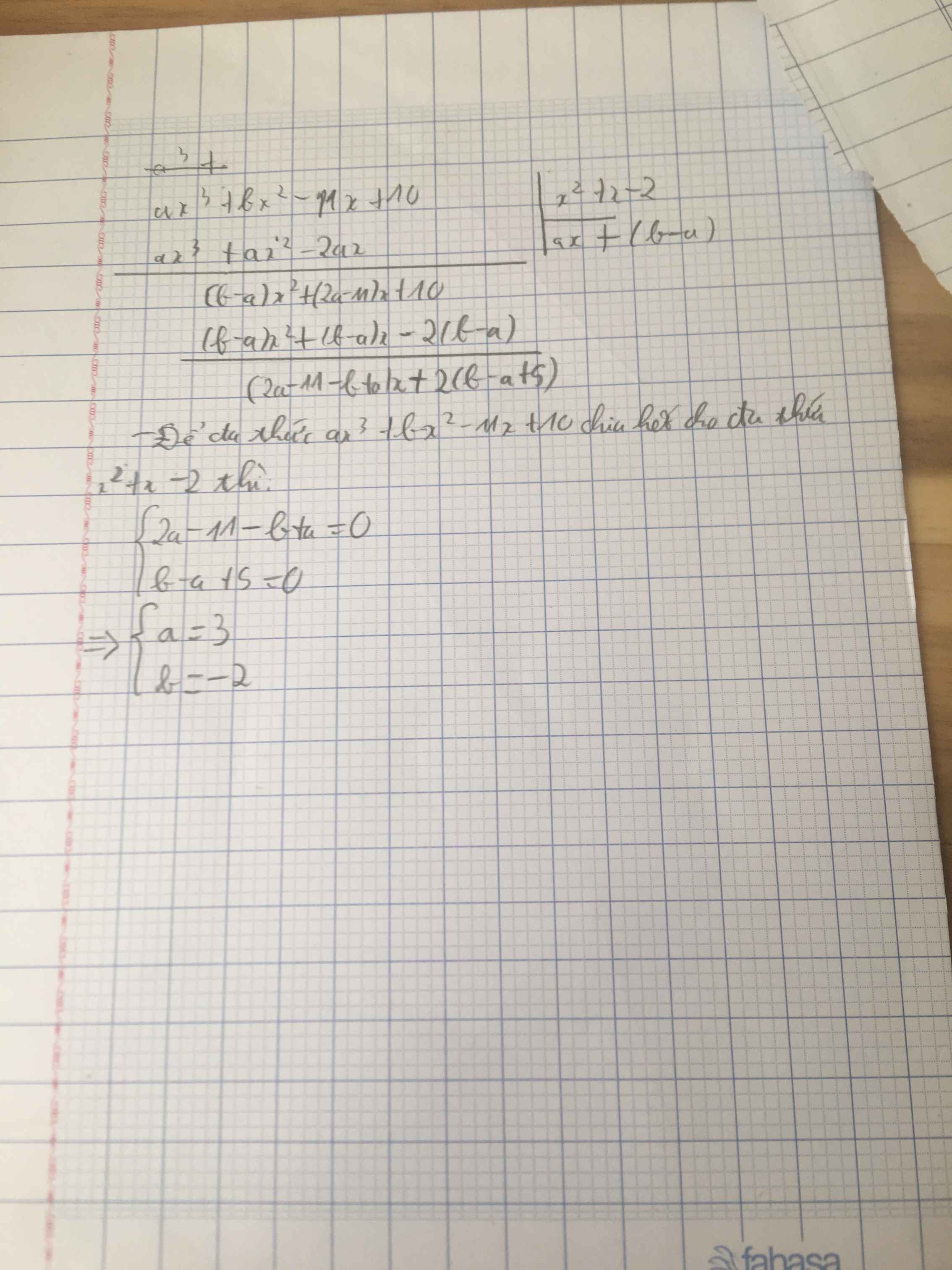K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
MT
0

Các câu hỏi dưới đây có thể giống với câu hỏi trên
DN
0

HH
2

AH
Akai Haruma
Giáo viên
30 tháng 1 2022
Lời giải:
Đặt $f(x)=ax^3+bx^2-11x+10$
$x^2+x-2=(x-1)(x+2)$
Do đó để $f(x)\vdots x^2+x-2$ thì $f(x)\vdots x-1$ và $f(x)\vdots x+2$
$\Leftrightarrow f(1)=f(-2)=0$ (theo định lý Bê-du về phép chia đa thức)
$\Leftrightarrow a+b-1=-8a+4b+32=0$
$\Leftrightarrow a=3; b=-2$

XO
22 tháng 7 2021
Ta có (ax3 + bx2 - 11x + 30) : (x2 - 3x - 10) = ax + 3a + b (dư (19a +3b - 11)x + 10(b + 3a +3)]
Để (ax3 + bx2 - 11x + 30) \(⋮\) (x2 - 3x - 10) khi \(\hept{\begin{cases}19a+3b-11=0\\b+3a+3=0\end{cases}}\Leftrightarrow\hept{\begin{cases}a=2\\b=-9\end{cases}}\)
Vậy a = 2 ; b = -9
HT
0

DM
0