K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 1 2022
\(9x^4-10x^2+1=0\\ \Rightarrow\left(9x^4-9x^2\right)-\left(x^2-1\right)=0\\ \Rightarrow9x^2\left(x^2-1\right)-\left(x^2-1\right)=0\\ \Rightarrow\left(x-1\right)\left(x+1\right)\left(9x^2-1\right)=0\\ \Rightarrow\left(x-1\right)\left(x+1\right)\left(3x-1\right)\left(3x+1\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=1\\x=-1\\x=\dfrac{1}{3}\\x=-\dfrac{1}{3}\end{matrix}\right.\)
23 tháng 1 2022
Đặt x^2 = t ( t>= 0 )
9t^2 - 10t + 1 = 0
ta có : a + b + c = 9 - 10 + 1 = 0
=> t = 1 ; t = 1/9
theo cách đặt x = 1 ; x = 1/3
PT
1
CM
24 tháng 12 2018
9x4 – 10x2 + 1 = 0 (1)
Đặt x2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành : 9t2 – 10t + 1 = 0 (2)
Giải (2):
Có a = 9 ; b = -10 ; c = 1
⇒ a + b + c = 0
⇒ Phương trình (2) có nghiệm t1 = 1; t2 = c/a = 1/9.
Cả hai nghiệm đều thỏa mãn điều kiện.
+ Với t = 1 ⇒ x2 = 1 ⇒ x = 1 hoặc x = -1.
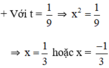
Vậy phương trình (1) có tập nghiệm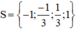 
CM
22 tháng 9 2017
a) 9 x 4 − 10 x 2 + 1 = 0 ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 9 t 2 − 10 t + 1 = 0 ( 2 )
Giải (2):
Có a = 9 ; b = -10 ; c = 1
⇒ a + b + c = 0
⇒ Phương trình (2) có nghiệm t 1 = 1 ; t 2 = c / a = 1 / 9
Cả hai nghiệm đều thỏa mãn điều kiện.
+ Với t = 1 ⇒ x 2 = 1 ⇒ x = 1 hoặc x = -1.
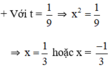
Vậy phương trình (1) có tập nghiệm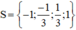 
b)
5 x 4 + 2 x 2 - 16 = 10 - x 2 ⇔ 5 x 4 + 2 x 2 - 16 - 10 + x 2 = 0 ⇔ 5 x 4 + 3 x 2 - 26 = 0
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 5 t 2 + 3 t − 26 = 0 ( 2 )
Giải (2) :
Có a = 5 ; b = 3 ; c = -26
⇒ Δ = 3 2 − 4.5 ⋅ ( − 26 ) = 529 > 0
⇒ Phương trình có hai nghiệm phân biệt
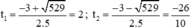
Đối chiếu điều kiện chỉ có t 1 = 2 thỏa mãn
+ Với t = 2 ⇒ ⇒ x 2 = 2 ⇒ x = √2 hoặc x = -√2.
Vậy phương trình (1) có tập nghiệm S = {-√2; √2}
c) 0 , 3 x 4 + 1 , 8 x 2 + 1 , 5 = 0 ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó, (1) trở thành : 0 , 3 t 2 + 1 , 8 t + 1 , 5 = 0 ( 2 )
Giải (2) :
có a = 0,3 ; b = 1,8 ; c = 1,5
⇒ a – b + c = 0
⇒ Phương trình có hai nghiệm t 1 = − 1 và t 2 = − c / a = − 5
Cả hai nghiệm đều không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.
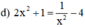
Điều kiện xác định: x ≠ 0.
Quy đồng, khử mẫu ta được :
2 x 4 + x 2 = 1 − 4 x 2 ⇔ 2 x 4 + x 2 + 4 x 2 − 1 = 0 ⇔ 2 x 4 + 5 x 2 − 1 = 0 ( 1 )
Đặt t = x 2 , điều kiện t > 0.
Khi đó (1) trở thành : 2 t 2 + 5 t - 1 = 0 ( 2 )
Giải (2) :
Có a = 2 ; b = 5 ; c = -1
⇒ Δ = 5 2 − 4.2 ⋅ ( − 1 ) = 33 > 0
⇒ Phương trình có hai nghiệm phân biệt:
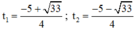
Đối chiếu với điều kiện thấy có nghiệm t 1 thỏa mãn.
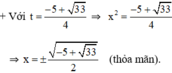
Vậy phương trình có tập nghiệm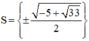 
NT
1
VH
17 tháng 7 2019
Đặt \(\sqrt{x^2+4x+7}=t>0\), ta có pt sau:
\(2\left(t^2+3\right)-7t=0\)
⇔ \(t^2-7t+6=0\Leftrightarrow\left(t-2\right)\left(2t-3\right)=0\)
⇔\(\left[{}\begin{matrix}t=2\\t=\frac{3}{2}\end{matrix}\right.\)⇔\(\left[{}\begin{matrix}x^2+4x+7=4\\x^2+4x+7=\frac{9}{4}\end{matrix}\right.\)⇔\(\left[{}\begin{matrix}\left[{}\begin{matrix}x=-1\\x=-3\end{matrix}\right.\\x=\frac{\pm\sqrt{79}-4}{2}\end{matrix}\right.\)
Vậy ...
