K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 10 2019
a/ \(\Leftrightarrow x^2+5x-2-2\sqrt[3]{x^2+5x-2}+4=0\)
Đặt \(\sqrt[3]{x^2+5x-2}=a\)
\(a^3-2a+4=0\)
\(\Leftrightarrow\left(a+2\right)\left(a^2-2a+2\right)=0\Rightarrow a=-2\)
\(\Rightarrow\sqrt[3]{x^2+5x-2}=-2\Rightarrow x^2+5x+6=0\Rightarrow...\)
b/ ĐKXĐ:...
\(\Leftrightarrow-3\left(-x^2+4x+10\right)-5\sqrt{-x^2+4x+10}+42=0\)
Đặt \(\sqrt{-x^2+4x+10}=a\ge0\)
\(-3a^2-5a+42=0\Rightarrow\left[{}\begin{matrix}a=3\\a=-\frac{14}{3}\left(l\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt{x^2+4x+10}=3\Rightarrow x^2-4x-1=0\Rightarrow...\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 10 2019
c/ ĐKXĐ: ...
\(\Leftrightarrow x^2+3x+3\sqrt{x^2+3x}-10=0\)
Đặt \(\sqrt{x^2+3x}=a\ge0\)
\(a^2+3a-10=0\Rightarrow\left[{}\begin{matrix}a=2\\a=-5\left(l\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt{x^2+3x}=2\Rightarrow x^2+3x-4=0\)
d/ ĐKXĐ: \(-1\le x\le2\)
\(\Leftrightarrow\sqrt{3-x+x^2}=1+\sqrt{2+x-x^2}\)
\(\Leftrightarrow3-x+x^2=3+x-x^2+2\sqrt{2+x-x^2}\)
\(\Leftrightarrow2+x-x^2+\sqrt{2+x-x^2}-2=0\)
Đặt \(\sqrt{2+x-x^2}=a\ge0\)
\(a^2+a-2=0\Rightarrow\left[{}\begin{matrix}a=1\\a=-2\left(l\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt{2+x-x^2}=1\Leftrightarrow x^2-x-1=0\)
e/ \(\Leftrightarrow\sqrt{x^2-3x+3}-1+\sqrt{x^2-3x+6}-2=0\)
\(\Leftrightarrow\frac{x^2-3x+2}{\sqrt{x^2-3x+3}+1}+\frac{x^2-3x+2}{\sqrt{x^2-3x+6}+2}=0\)
\(\Leftrightarrow\left(x^2-3x+2\right)\left(\frac{1}{\sqrt{x^2-3x+3}+1}+\frac{1}{\sqrt{x^2-3x+6}+2}\right)=0\)
\(\Leftrightarrow x^2-3x+2=0\)
TN
1
28 tháng 1 2023
a: ĐKXĐ: x^2-2x<>0 và x^2-1>0
=>(x>1 và x<>2) hoặc x<-1
b: ĐKXĐ: x+1>0 và 5-3x>0
=>x>-1 và 3x<5
=>-1<x<5/3
c: DKXĐ: 5x+3>=0 và 3-x>0
=>x>=-3/5 và x<3
=>-3/5<=x<3
d: ĐKXĐ: 4-x^2>0 và 1+x>=0
=>x^2<4 và x>=-1
=>-2<x<2 và x>=-1
=>-1<=x<2
e: ĐKXĐ: 2-3x<>0 và 1-6x>0
=>x<>2/3 và x<1/6
=>x<1/6
3 tháng 2 2019
đa phần mình sử dụng phương pháp liên hợp nha bạn
\(\sqrt{a}-\sqrt{b}=\dfrac{a-b}{\sqrt{a}+\sqrt{b}}\)
b. điều kiện \(\dfrac{1}{4}\le x\le\dfrac{3}{8}\), pt:
\(\Leftrightarrow\sqrt{3-8x}-\sqrt{4x-1}=6x-2\\ \Leftrightarrow\dfrac{3-8x-4x+1}{\sqrt{3-8x}+\sqrt{4x-1}}=2\left(3x-1\right)\\ \Leftrightarrow\dfrac{-4\left(3x-1\right)}{\sqrt{3-8x}+\sqrt{4x-1}}=2\left(3x-1\right)\\ \Leftrightarrow2\left(3x-1\right)+\dfrac{4\left(3x-1\right)}{\sqrt{3-8x}+\sqrt{4x-1}}=0\\ \Leftrightarrow2\left(3x-1\right)\left(1+\dfrac{2}{\sqrt{3-8x}+\sqrt{4x-1}}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\left(n\right)\\1+\dfrac{2}{\sqrt{3-8x}+\sqrt{4x-1}}=0\left(vn\right)\end{matrix}\right.\)
d. điều kiện: \(x\le-4\cup x\ge0\), pt:
\(\Leftrightarrow1-\sqrt{x^2-3x+3}=\sqrt{2x^2+x+2}-\sqrt{x^2+4x}\\ \Leftrightarrow\dfrac{1-x^2+3x-3}{1+\sqrt{x^2-3x+3}}=\dfrac{2x^2+x+2-x^2-4x}{\sqrt{2x^2+x+2}+\sqrt{x^2+4x}}\\ \Leftrightarrow\dfrac{-\left(x-1\right)\left(x-2\right)}{1+\sqrt{x^2-3x+3}}=\dfrac{\left(x-1\right)\left(x-2\right)}{\sqrt{2x^2+x+2}+\sqrt{x^2+4x}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(n\right)\\x=1\left(n\right)\\\dfrac{-1}{1+\sqrt{x^2-3x+3}}=\dfrac{1}{\sqrt{2x^2+x+2}+\sqrt{x^2+4x}}\left(vn\right)\end{matrix}\right.\)
e. điều kiện:x thuộc R
\(\Leftrightarrow\sqrt{x^2+15}-4=3x-3+\sqrt{x^2+8}-3\\ \Leftrightarrow\dfrac{x^2+15-16}{\sqrt{x^2+15}+4}=3\left(x-1\right)+\dfrac{x^2+8-9}{\sqrt{x^2+8}+3}\\ \Leftrightarrow\dfrac{\left(x-1\right)\left(x+1\right)}{\sqrt{x^2+15}+4}-3\left(x-1\right)-\dfrac{\left(x-1\right)\left(x+1\right)}{\sqrt{x^2+8}+3}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\\dfrac{\left(x+1\right)}{\sqrt{x^2+15}+4}-3-\dfrac{\left(x+1\right)}{\sqrt{x^2+8}+3}=0\left(1\right)\end{matrix}\right.\)
(1) mình không biết có vô nghiệm không nữa và cũng thua luôn
f. điều kiện: \(x\ge-2\)
bài này giải cách hơi khác một chút
đặt \(a=\sqrt{x+5}\left(\ge0\right)\\ b=\sqrt{x+2}\left(\ge0\right)\)
pt:
\(\Leftrightarrow\left(\sqrt{x+5}-\sqrt{x+2}\right)\left[\left(1+\sqrt{\left(x+5\right)\left(x+2\right)}\right)\right]\\ \Rightarrow\left(a-b\right)\left(1+ab\right)=3\left(1\right)\)
mà \(a^2-b^2=x+5-x-2=3\\ \Rightarrow\left(a-b\right)\left(a+b\right)=3\left(2\right)\)
=> (1) = (2)
\(\Leftrightarrow\left(a-b\right)\left(1+ab\right)=\left(a-b\right)\left(a+b\right)\\ \Leftrightarrow\left(a-b\right)\left(1+ab-a-b\right)=0\\ \Leftrightarrow\left(a-b\right)\left(a-1\right)\left(b-1\right)=0\)
TH1: a=b \(\Leftrightarrow\sqrt{x+5}=\sqrt{x+2}\Leftrightarrow x+5=x+2\left(vn\right)\)
TH2: a=1\(\Leftrightarrow\sqrt{x+5}=1\Leftrightarrow x=-4\left(l\right)\)
TH3: b=1\(\Leftrightarrow\sqrt{x+2}=1\Leftrightarrow x=-1\left(n\right)\)
g. điều kiện: \(x\le-\sqrt{2}\cup x\ge\dfrac{7+\sqrt{37}}{2}\)
pt:
\(\dfrac{3x^2-7x+3-3x^2+5x+1}{\sqrt{3x^2-7x+2}+\sqrt{x^2-3x-4}}=\dfrac{x^2-2-x^2+3x-4}{\sqrt{3x^2-5x-1}+\sqrt{x^2-2}}\\ \Leftrightarrow\dfrac{-2\left(x-2\right)}{\sqrt{3x^2-7x+2}+\sqrt{x^2-3x-4}}=\dfrac{3\left(x-2\right)}{\sqrt{3x^2-5x-1}+\sqrt{x^2-2}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\left(n\right)\\\dfrac{-2}{\sqrt{3x^2-7x+2}+\sqrt{x^2-3x-4}}=\dfrac{3}{\sqrt{3x^2-5x-1}+\sqrt{x^2-2}}\left(vn\right)\end{matrix}\right.\)h. điều kiện \(x\le-2-\sqrt{7}\cup x\ge-2+\sqrt{7}\)
\(\sqrt{2x^2+x-1}-\sqrt{x^2+4x-3}=\sqrt{2x^2+4x-3}-\sqrt{3x^2+x-1}\\ \Leftrightarrow\dfrac{2x^2+x-1-x^2-4x+3}{\sqrt{2x^2+x-1}+\sqrt{x^2+4x-3}}=\dfrac{2x^2+4x-3-3x^2-x+1}{\sqrt{2x^2+4x-3}+\sqrt{3x^2+x-1}}\\ \Leftrightarrow\dfrac{x^2-3x+2}{\sqrt{2x^2+x-1}+\sqrt{x^2+4x-3}}=\dfrac{-\left(x^2-3x+2\right)}{\sqrt{2x^2+4x-3}+\sqrt{3x^2+x-1}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-3x+2=0\Leftrightarrow x=1\left(n\right),x=2\left(n\right)\\\dfrac{1}{\sqrt{2x^2+x-1}+\sqrt{x^2+4x-3}}=\dfrac{-1}{\sqrt{2x^2+4x-3}+\sqrt{3x^2+x-1}}\left(vn\right)\end{matrix}\right.\)
(nhớ tích cho mình nha, mấy bài kia mình ko biết làm huhu)
HN
25 tháng 2 2017
1/ \(3x^2+4x-3=4x\sqrt{4x-3}\)
\(\Leftrightarrow\left(4x^2-4x\sqrt{4x-3}+4x-3\right)-x^2=0\)
\(\Leftrightarrow\left(2x-\sqrt{4x-3}\right)^2-x^2=0\)
\(\Leftrightarrow\left(3x-\sqrt{4x-3}\right)\left(x-\sqrt{4x-3}\right)=0\)
\(\Leftrightarrow\left[\begin{matrix}3x=\sqrt{4x-3}\\x=\sqrt{4x-3}\end{matrix}\right.\)
\(\Leftrightarrow\left[\begin{matrix}9x^2-4x+3=0\\x^2-4x+3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[\begin{matrix}x=1\\x=3\end{matrix}\right.\)
H
17 tháng 6 2019
3.\(pt\Leftrightarrow\sqrt{3x+8}-\sqrt{3x+5}=\sqrt{5x-4}-\sqrt{5x-7}\)
\(\Leftrightarrow\frac{3x+8-5x+4}{\sqrt{3x+8}+\sqrt{5x+4}}-\frac{3x+5-5x+7}{\sqrt{3x+5}+\sqrt{5x+7}}=0\)
\(\Leftrightarrow\left(12-2x\right)\left(\frac{1}{\sqrt{3x+8}+\sqrt{5x+4}}+\frac{1}{\sqrt{3x+5}+\sqrt{5x+7}}\right)=0\)
\(\Rightarrow x=6\)
20 tháng 3 2020
28. \(x^2+\frac{9x^2}{\left(x-3\right)^2}=40\) DK: \(x\ne3\)
PT\(\Leftrightarrow\left(x+\frac{3x}{x-3}\right)^2-6\frac{x^2}{x-3}-40=0\)\(\Leftrightarrow\frac{x^4}{\left(x-3\right)^2}-6\frac{x^2}{x-3}-40=0\)
Dat \(\frac{x^2}{x-3}=a\). PTTT \(a^2-6a-40=0\)\(\Leftrightarrow\left(a-10\right)\left(a+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=10\\a=-4\end{matrix}\right.\)
giai tiep
20 tháng 3 2020
14. \(\frac{1}{\sqrt{x}+1}+\frac{1}{\sqrt{x}-1}=1\) DK: \(\left\{{}\begin{matrix}x\ge0\\x\ne1\end{matrix}\right.\)
PT\(\Leftrightarrow\frac{\sqrt{x}-1+\sqrt{x}+1}{x-1}=1\Leftrightarrow2\sqrt{x}=x-1\)\(\Leftrightarrow x-2\sqrt{x}+1=2\Leftrightarrow\left(\sqrt{x}-1\right)^2=2\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3+2\sqrt{2}\\x=3-2\sqrt{2}\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 10 2019
a/ ĐKXĐ: \(x^2+3x+2\ge0\)
\(\Leftrightarrow3-2\sqrt{x^2+3x+2}=1-2\sqrt{x^2-x+1}\)
\(\Leftrightarrow\sqrt{x^2+3x+2}=\sqrt{x^2-x+1}+1\)
\(\Leftrightarrow x^2+3x+2=x^2-x+1+1+2\sqrt{x^2-x+1}\)
\(\Leftrightarrow2x=\sqrt{x^2-x+1}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\4x^2=x^2-x+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\3x^2+x-1=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=\frac{-1+\sqrt{13}}{6}\\x=\frac{-1-\sqrt{13}}{6}\left(l\right)\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 10 2019
b/ ĐKXĐ: \(3x^2-7x+2\ge0\)
\(\Leftrightarrow\sqrt{3x^2-5x+7}=3-\sqrt{3x^2-7x+2}\) (1)
\(\Rightarrow3x^2-5x+7=9+3x^2-7x+2-6\sqrt{3x^2-7x+2}\)
\(\Rightarrow2-x=3\sqrt{3x^2-7x+2}\) (\(x\le2\))
\(\Rightarrow\left(2-x\right)^2=9\left(3x^2-7x+2\right)\)
\(\Rightarrow x^2-4x+4=27x^2-63x+18\)
\(\Rightarrow26x^2-59x+14=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=\frac{7}{26}\end{matrix}\right.\)
Do bước biến đổi thứ 2 ko phải phép tương đương nên cần thay 2 nghiệm vào (1) để kiểm tra lại, bạn tự thay nhé
(x+5)(2-x)=3\(\sqrt{x^2+3x}\)
<=> -x2-3x+10= 3\(\sqrt{x^2+3x}\)
⇔ x2 + 3x + 3√(x2 + 3x) - 10 = 0
Đặt t = √(x2 + 3x), t ≥ 0. Phương trình đã cho trở thành
t2 + 3t - 10 = 0 ⇔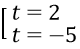
Vì t ≥ 0 ⇒ t = 2, thay vào ta có √(x2 + 3x) = 2
⇔ x2 + 3x - 4 = 0 ⇔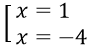
Vậy phương trình có nghiệm là x = 1 và x = -4