K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
1
GT
5
1 tháng 5 2019
Bài này quá dễ
x/40 - x/50= 1/3
<=>5x/200 - 4x/200=1/3
<=> x/200= 1/3
<=> x= 200/3.
GT
1 tháng 5 2019
bạn ê, mik bị ngu toán, lười suy nghĩ ấy mà nên đừng nói dễ hay khó j vs mik
1 tháng 6 2021
Giải pt à bạn:P?
\(\left(x+4\right)\left(x^2-4x+16\right)-\left(x-2\right)^3=0\)
\(\Leftrightarrow x^3+4^3-\left(x^3-8-6x^2+12x\right)=0\)
\(\Leftrightarrow x^3+4^3-x^3+8+6x^2-12x=0\)
\(\Leftrightarrow72+6x^2-12x=0\Leftrightarrow6\left(x^2-2x+12\right)=0\Leftrightarrow x^2-2x+12=0\)
Ta lại có: \(x^2-2x+12=x^2-2x+1+11=\left(x-1\right)^2+11\ge11>0\ne0\)
=> Pt vô nghiệm.
2
10 tháng 5 2022
`[x+1]/2021+[x+2]/2020+[x+3]/2019+[x+4]/2018=-4`
`<=>[x+1]/2021+1+[x+2]/2020+1+[x+3]/2019+1+[x+4]/2018+1=-4+4`
`<=>[x+1+2021]/2021+[x+2+2020]/2020+[x+3+2019]/2019+[x+4+2018]/2018=0`
`<=>[x+2022]/2021+[x+2022]/2020+[x+2022]/2019+[x+2022]/2018=0`
`<=>(x+2022)(1/2021+2020+1/2019+1/2018)=0`
Mà `1/2021+2020+1/2019+1/2018 \ne 0`
`=>x+2022=0`
`<=>x=-2022`
Vậy `S={-2022}`
17 tháng 2 2022
Bài 2:
Xét ΔBDC có BE/ED=BF/FC
nên EF//DC
mà DC//AB
nên EF//AB
NL
0
11 tháng 3 2022
a: Xét ΔADH vuông tại H và ΔBDA vuông tại A có
\(\widehat{ADH}\) chung
Do đó: ΔADH∼ΔBDA
b: Xét ΔHAD vuông tại H và ΔHBA vuông tại H có
\(\widehat{HAD}=\widehat{HBA}\)
Do đó: ΔHAD∼ΔHBA
Suy ra: HA/HB=HD/HA
hay \(HA^2=HB\cdot HD\)
11 tháng 3 2022
a) Xét \(\Delta ADH\) và \(\Delta BDA:\)
\(\widehat{H}=\widehat{A}\left(=90^o\right).\)
\(\widehat{D}\) chung.
\(\Rightarrow\Delta ADH\sim\Delta BDA\left(g-g\right).\)
b) Xét \(\Delta BDA\) và \(\Delta BAH:\)
\(\widehat{BAD}=\widehat{BHA}\left(=90^o\right).\)
\(\widehat{B}\) chung.
\(\Rightarrow\Delta BDA\sim\) \(\Delta BAH\left(g-g\right).\)
Mà \(\Delta ADH\sim\Delta BDA\left(cmt\right).\)
\(\Rightarrow\Delta ADH\sim\Delta BAH.\)
\(\Rightarrow\dfrac{AH}{BH}=\dfrac{DH}{AH}\) (2 cạnh tương ứng).
\(\Rightarrow AH^2=DH.BH.\)
KN
15 tháng 1 2020
\(ĐKXĐ:a,b,c\ne0\)
\(\frac{x-a}{bc}+\frac{x-b}{ca}+\frac{x-c}{ab}=\frac{2}{a}+\frac{2}{b}+\frac{2}{c}\)
\(\Leftrightarrow\frac{xa-a^2}{abc}+\frac{xb-b^2}{abc}+\frac{xc-c^2}{abc}=\frac{2bc}{abc}+\frac{2ac}{abc}+\frac{2ab}{abc}\)
\(\Leftrightarrow\frac{xa-a^2+xb-b^2+xc-c^2}{abc}=\frac{2bc+2ac+2ab}{abc}\)
\(\Leftrightarrow xa-a^2+xb-b^2+xc-c^2=2bc+2ac+2ab\)
\(\Leftrightarrow xa+xb+xc=2bc+2ac+2ab+a^2+b^2+c^2\)
\(\Leftrightarrow x\left(a+b+c\right)=\left(a+b+c\right)^2\)
\(\Leftrightarrow x=a+b+c\)
Vậy x = a + b + c
KN
15 tháng 1 2020
\(ĐKXĐ:a,b,c\ne0\)
\(\frac{a+b-x}{c}+\frac{b+c-x}{a}+\frac{c+a-x}{b}+\frac{4x}{a+b+c}=1\)
\(\Leftrightarrow\frac{a+b-x}{c}+\frac{b+c-x}{a}+\frac{c+a-x}{b}=1-\frac{4x}{a+b+c}\)
\(\Leftrightarrow1+\frac{a+b-x}{c}+1+\frac{b+c-x}{a}+1+\frac{c+a-x}{b}=4\)
\(-\frac{4x}{a+b+c}\)
\(\Leftrightarrow\frac{a+b+c-x}{c}+\frac{a+b+c-x}{a}+\frac{a+b+c-x}{b}=\)
\(\frac{4\left(a+b+c\right)}{a+b+c}-\frac{4x}{a+b+c}\)
\(\Leftrightarrow\frac{a+b+c-x}{c}+\frac{a+b+c-x}{a}+\frac{a+b+c-x}{b}=\)
\(\frac{4\left(a+b+c-x\right)}{a+b+c}\)
\(\Leftrightarrow\left(a+b+c-x\right)\left(\frac{1}{c}+\frac{1}{a}+\frac{1}{b}-\frac{4}{a+b+c}\right)=0\)
\(\Rightarrow\left(a+b+c-x\right)=0\)hoặc \(\left(\frac{1}{c}+\frac{1}{a}+\frac{1}{b}-\frac{4}{a+b+c}\right)=0\)
+) Nếu \(\Rightarrow\left(a+b+c-x\right)=0\)thì x = a + b + c
+) Nếu \(\left(\frac{1}{c}+\frac{1}{a}+\frac{1}{b}-\frac{4}{a+b+c}\right)=0\)thì x thỏa mãn với mọi số
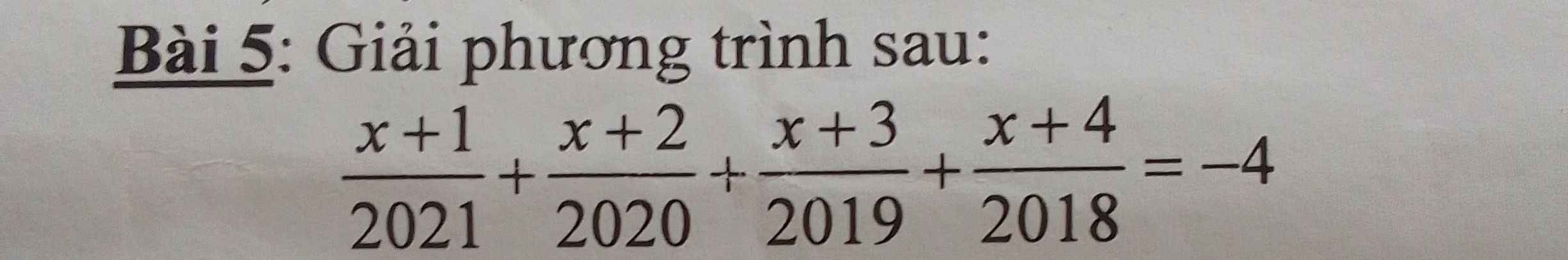
`x/40 - x/50 =0,3`
`<=> x/40-x/50 =3/10`
`<=> (5x)/200 - (4x)/200 = 60/200`
`<=> 5x-4x=60`
`<=>x=60`
Vậy phương trình có nghiệm `x=60`
\(\dfrac{x}{40}-\dfrac{x}{50}=0,3\)
\(\Leftrightarrow\dfrac{55x}{200}-\dfrac{4x}{200}=\dfrac{60}{200}\)
\(\Leftrightarrow x=60\)
\(\text{Vậy phương trình có tập nghiệm là }S=\left\{60\right\}\)