Question

[doducminh]

x²+y²=0

(x-1)²+(y+2)²=0

(x-11+y)²+(x-4-y)²=0

Answer 1

[T.Anh 2K7(siêu quậy)(тoáɴ๖ۣۜнọc)]

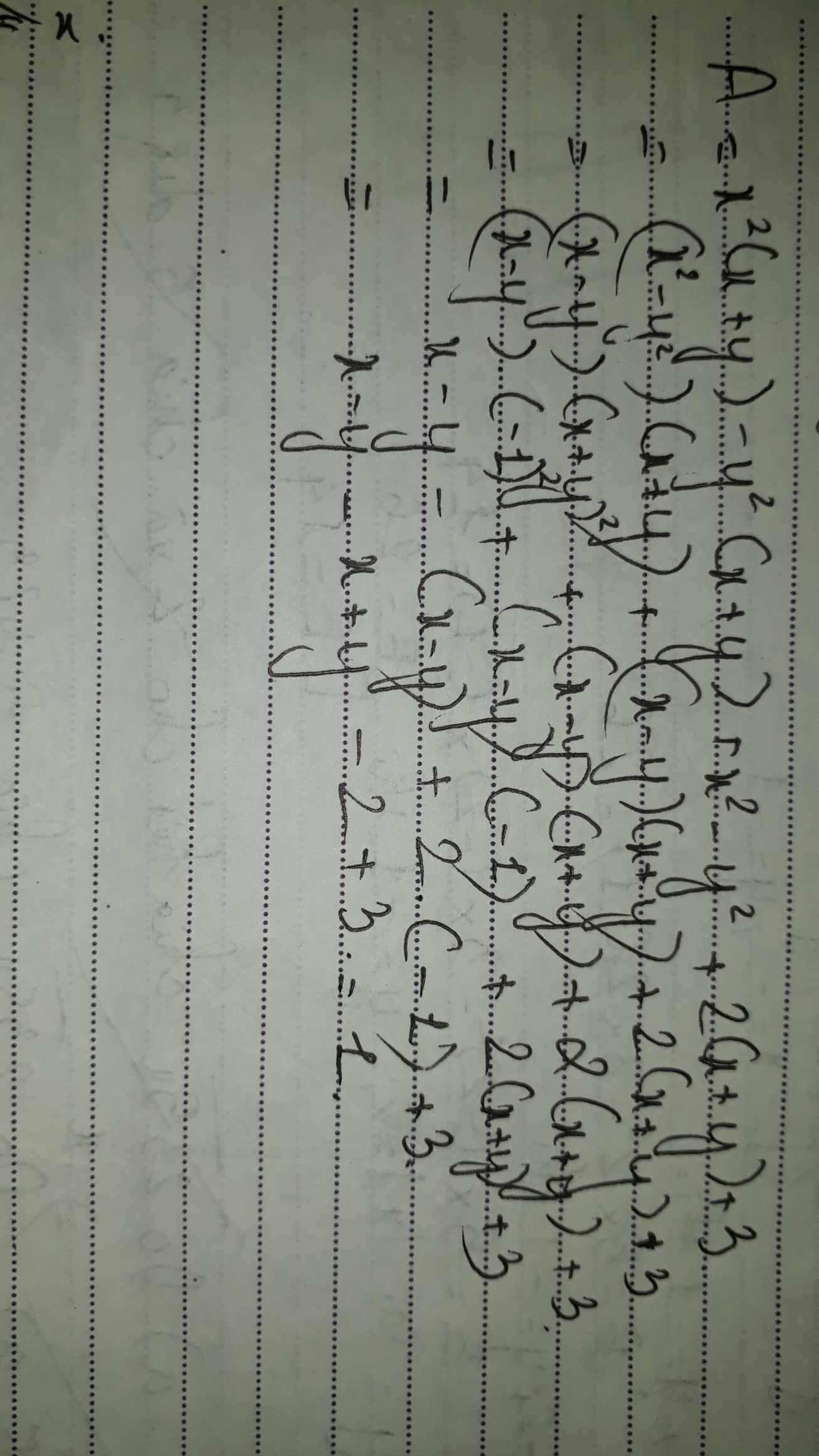
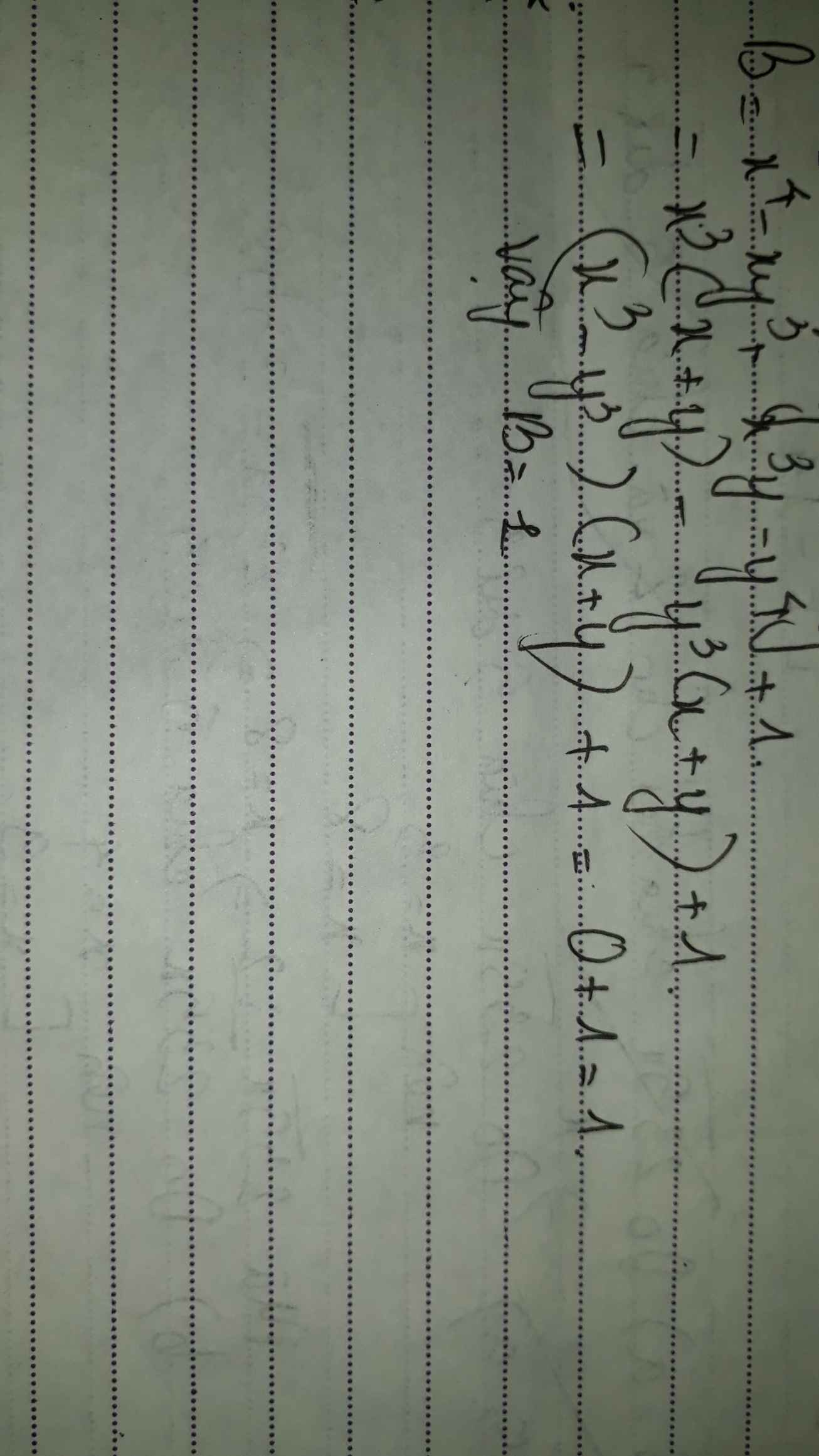
Ta có:\(x^2\ge0\forall x\)

      \(y^2\ge0\forall y\)

\(\Rightarrow x^2+y^2\ge0\)

Dấu = xaye ra khi và chỉ khi x=y=0

Ta có:\(\left(x-1\right)^2\ge0\forall x\)

       \(\left(y+2\right)^2\ge0\forall y\)

\(\Rightarrow\left(x-1\right)^2+\left(y+2\right)^2\ge0\)

Dấu = xảy ra khi và chỉ khi \(\hept{\begin{cases}x-1=0\Rightarrow x=1\\y+2=0\Rightarrow y=-2\end{cases}}\)

Ta có:\(\left(x-11+y\right)^2\ge0\forall x,y\)

      \(\left(x-4-y\right)^2\ge0\)

\(\Rightarrow\left(x-11+y\right)^2+\left(x-4-y\right)^2\ge0\)

Dấu = xaye ra khi và chỉ khi \(\hept{\begin{cases}x-11+y=0\Rightarrow x+y=11\\x-4-y=0\Rightarrow x-y=4\end{cases}}\)

\(\Rightarrow\hept{\begin{cases}x=\left(11+4\right):2=7,5\\y=11-7,5=3,5\end{cases}}\)

Answer 2

[$๖ۣۜN๖ۣۜE๖ۣۜV ๖ۣۜE ๖ۣۜR $ ^^๖ۣۜG๖ۣۜ...]

a)vì x^2 và y^2 luôn luôn lớn hớn hoặc bằng 0  (1)

mà x^2+y^2=0

<=>x,y=0

b) cũng từ (1)

mà (x-1)^2+(y+2)^2=0

=>x-1=0=>x=1

y+2=0=>y=-2

c)cũng từ 1

=>x-11+y=0       (2)

và x-4-y=0        (3)

vì x-11=x-4-7

vì (3)   là x-4-y

(2) là x-4-7+y  => không tồn tại x thõa mãn đề bài