
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\Leftrightarrow x-\left[3-x+3+x-2\right]=0\)
=>x=4

Hai bài bị trùng nhau nên các bạn nhìn ảnh hay văn bản đều như nhau ạ
c: =>x+2>0
hay x>-2
d: =>-4<=x<=3
e: =>\(x\in\varnothing\)
f: \(\Leftrightarrow\left[{}\begin{matrix}x>4\\x< -6\end{matrix}\right.\)

\(\left(x^2+1\right)\left(x-5\right)=0\\ \Rightarrow\left\{{}\begin{matrix}x^2+1=0\left(vô.lí.vì.x^2\ge0,1>0\right)\\x-5=0\end{matrix}\right.\\ \Rightarrow x=5\)
\(\left(x^2+1\right)\left(x-5\right)=0\)
TH1 : x^2 + 1 = 0 ( vô lí vì x^2 + 1 > 0 )
TH2 : x - 5 = 0 <=> x = 5
Vậy x = 5

\(10+2x=45\div4^5\)
\(10+2x=45\div1024\)
\(10+2x=\dfrac{45}{1024}\)
\(2x=\dfrac{45}{1024}-10\)
\(2x=-\dfrac{10195}{1024}\)
\(x=-\dfrac{10195}{1024}:2=-\dfrac{10195}{2048}\)

\(\Leftrightarrow-\dfrac{2}{5}\left(4x-3\right)^2=-\dfrac{5}{18}\)
\(\Leftrightarrow\left(4x-3\right)^2=\dfrac{25}{36}\)
\(\Leftrightarrow4x-3\in\left\{\dfrac{5}{6};-\dfrac{5}{6}\right\}\)
hay \(x\in\left\{\dfrac{23}{24};\dfrac{13}{24}\right\}\)

\(\Leftrightarrow y\left(x+1\right)+2\left(x+1\right)+9=0\)
\(\Leftrightarrow\left(x+1\right)\left(y+2\right)=-9\)
Để x;y nguyên thì:
\(\left\{{}\begin{matrix}x+1=3\\y+2=-3\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=-5\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x+1=-3\\y+2=3\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-4\\y=1\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x+1=1\\y+2=-9\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=-11\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x+1=-9\\y+2=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-10\\y=-1\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x+1=-1\\y+2=9\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=7\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x+1=9\\y+2=-1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=8\\y=-3\end{matrix}\right.\)

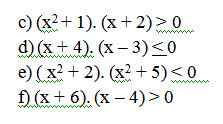 Giúp mình với, mình cần gấp ạ
Giúp mình với, mình cần gấp ạ
\(\Rightarrow\left[{}\begin{matrix}x+2=0\\x-4=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-2\\x=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+2=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\x=4\end{matrix}\right.\)