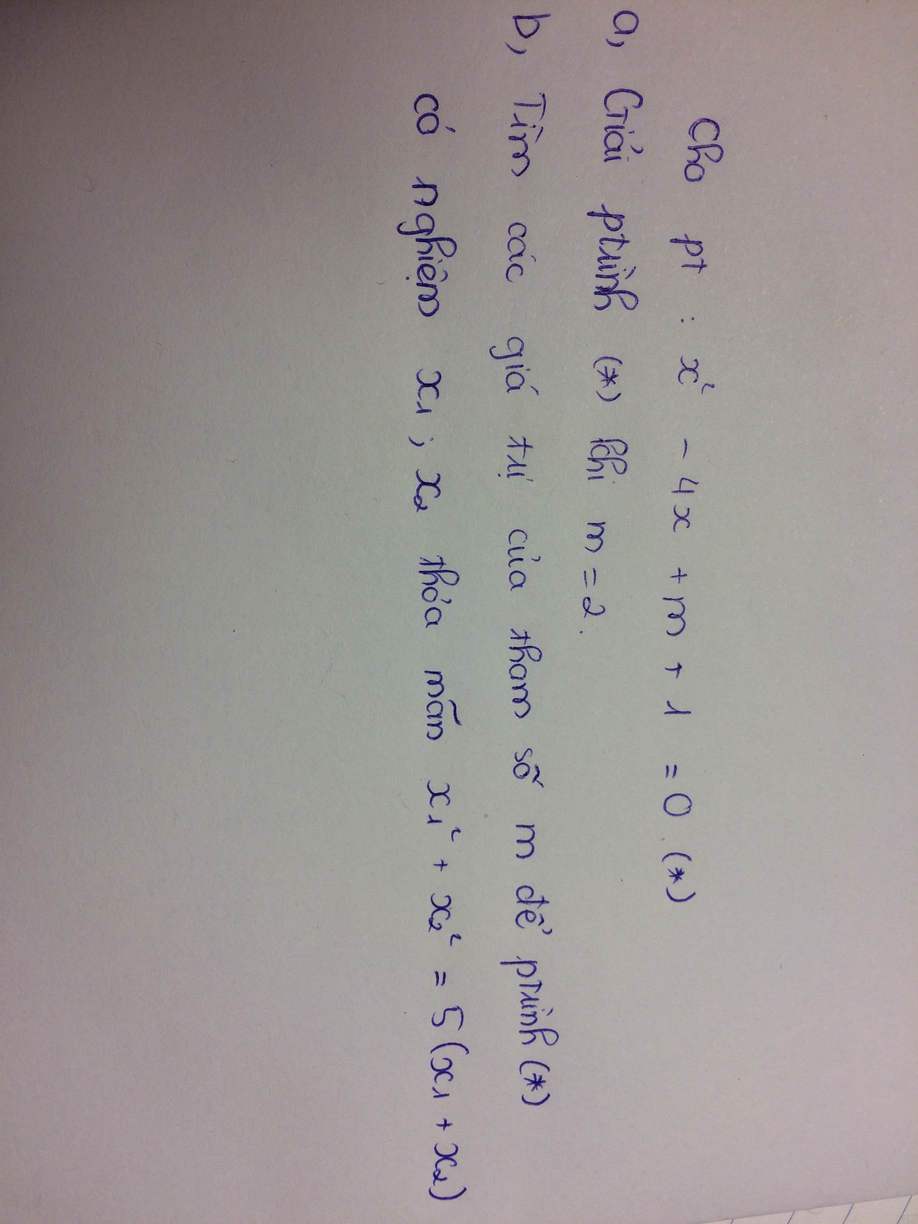K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
22 tháng 6 2018
Ta có: \(\hept{\begin{cases}\left(\frac{1}{x}+y\right)+\left(\frac{1}{x}-y\right)=\frac{5}{8}\\\left(\frac{1}{x}+y\right)-\left(\frac{1}{x}-y\right)=-\frac{3}{8}\end{cases}\Leftrightarrow\hept{\begin{cases}\frac{2}{x}=\frac{5}{8}\\2y=-\frac{3}{8}\end{cases}\Leftrightarrow}\hept{\begin{cases}x=\frac{16}{5}\\y=-\frac{3}{16}\end{cases}}}\)
93
0
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 4 2019
Vấn đề lớn nhất là không dịch được đề của bạn, nhìn chẳng khác gì mật mã cả
27 tháng 9 2021
b: \(\sqrt{8-2\sqrt{15}}-\sqrt{5}\)
\(=\sqrt{5}-\sqrt{3}-\sqrt{5}\)
\(=-\sqrt{3}\)
c: \(\sqrt{11-6\sqrt{2}}=3-\sqrt{2}\)
d: \(\sqrt{5-2\sqrt{6}}=\sqrt{3}-\sqrt{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 2 2022
\(\Delta'=4-\left(m+1\right)\ge0\Rightarrow m\le3\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=4\\x_1x_2=m+1\end{matrix}\right.\)
\(x_1^2+x_2^2=5\left(x_1+x_2\right)\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=5\left(x_1+x_2\right)\)
\(\Leftrightarrow16-2\left(m+1\right)=20\)
\(\Leftrightarrow m=-3\) (thỏa mãn)
AM
7 tháng 2 2022
a. Ta có: \(x^2-4x+m+1=0\)
Thay m=2 ta được: \(x^2-4x+2+1=0\Leftrightarrow x^2-4x+3=0\Leftrightarrow\left[{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)
b. Để phương trình có 2 nghiệm phân biệt thì \(\Delta=\left(-4\right)^2-4.1.\left(m+1\right)>0\)
\(\Leftrightarrow16-4\left(m+1\right)>0\Leftrightarrow16>4\left(m+1\right)\Leftrightarrow4>m+1\Leftrightarrow m< 3\)
Áp dụng định lí Vi-et ta có: \(\left\{{}\begin{matrix}x_1+x_2=4\\x_1x_2=m+1\end{matrix}\right.\)
Theo đề ta có: \(x_1^2+x_2^2=5\left(x_1+x_2\right)\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=5\left(x_1+x_2\right)\)
\(\Leftrightarrow\left(4\right)^2-2\left(m+1\right)=5.4\)
\(\Leftrightarrow16-2m-2=20\Leftrightarrow m=-3\) (TM)
