Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp:
Đặt 2x = t, t > 0. Chuyển về bài toán tìm m để phương trình bậc 2 ẩn t có 2 nghiệm t1, t2 thỏa mãn t1.t2 = 8
Cách giải:

Để phương trình (1) có 2 nghiệm x1, x2 thỏa mãn x1 + x2 = 3 thì phương trình (2) có 2 nghiệm t1,t2 thỏa mãn t1.t2 = 2x1.2x2 = 2x1 + x2 = 23 = 8
Khi đó:
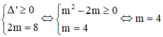

Đáp án A
Ghi nhớ: Nếu hàm số ![]()
liên tục trên đoạn ![]() và
và ![]() thì phương trình
thì phương trình ![]()
có ít nhất một nghiệm nằm trong khoảng ![]() .
.

\(2021^x=t>0\Rightarrow t^2-22t+2021-m=0\)
Pt có 2 nghiệm nên (1) có 2 nghiệm dương \(\Rightarrow\left\{{}\begin{matrix}\Delta'=121-\left(2021-m\right)\ge0\\t_1+t_2=22>0\\t_1t_2=2021-m>0\end{matrix}\right.\) (1)
\(x=log_{2021}t\Rightarrow x_1+x_2=log_{2021}t_1+log_{2021}t_2=log_{2021}\left(t_1t_2\right)\)
\(\Rightarrow log_{2021}\left(t_1t_2\right)\ge\dfrac{1}{2}\Rightarrow t_1t_2\ge\sqrt{2021}\)
\(\Rightarrow2021-m\ge\sqrt{2021}\) (2)
(1);(2) \(\Rightarrow m\)

Đáp án D.
Đặt t = log3 x => t2 – 3t + 2m – 7 = 0
PT có 2 nghiệm khi ∆ = 9 - 4 2 m - 7 = 37 - 8 m > 0
=> PT có 2 nghiệm t1; t2
⇒ log 3 x 1 = t 1 log 3 x 2 = t 2 ⇒ x 1 = 3 t 1 x 2 = 3 t 2
Khi đó theo định lý Viet ta có:
t 1 + t 2 = 3 t 1 . t 2 = 2 m - 7
Do

Đặt
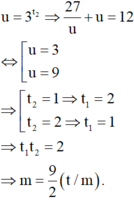




\(ac=-2\left(m^2+8\right)< 0\Rightarrow\) pt luôn có 2 nghiệm pbn trái dấu
Theo Viet ta có: \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=-2\left(m^2+8\right)\end{matrix}\right.\)
\(A=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2\)
\(A=m^2+4\left(m^2+8\right)=5m^2+32\ge32\)
\(\Rightarrow A_{min}=32\) khi \(m=0\)