Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Đặt $A=10^n+18^n$.
Nếu $n=0$ thì $A$ chia $27$ dư $2$
Nếu $n=1$ thì $A=28$ chia $27$ dư $1$
Nếu $n\geq 2$. Xét các TH sau
TH1: Nếu $n=3k$ ( $k\in\mathbb{N} >1$)
Có \(10^{3}\equiv 1\pmod {27}\Rightarrow 10^n=(10^3)^k\equiv 1\pmod {27}\)
\(18^n=18^{3k}\equiv (-9)^{3k}\equiv 0\pmod{27}\)
\(\Rightarrow A\equiv 1\pmod{27}\), tức $A$ chia $27$ dư $1$
TH2: $n=3k+1$ ( $k\in\mathbb{N} >1$)
\(10^{n}=10^{3k+1}=10^{3k}.10\equiv 1.10\equiv 10\pmod {27}\)
\(18^{n}=18^{3k+1}\equiv (-9)^{3k+1}\equiv 0\pmod{27}\)
\(\Rightarrow A\equiv 10\pmod{27}\)
TH3: $n=3k+2$
\(10^{n}=10^{3k+2}=10^{3k}.100\equiv 100\equiv 19\pmod{27}\)
\(18^n=18^{3k+2}\equiv (-9)^{3k+2}\equiv 0\pmod {27}\)
\(\Rightarrow A\equiv 19\pmod {27}\)


Lời giải:
Xét modulo $3$ cho $n$ thôi . Ở đây mình xét cụ thể TH $n=3k$. TH \(n=3k+1,3k+2\) ta hoàn toàn làm tương tự
TH1: \(n=3k\)
Ta có :
\(11^3\equiv 1\pmod 7\Rightarrow 11^n=11^{3k}\equiv 1\pmod 7\Rightarrow 11^{n+2}\equiv 11^2\equiv 2\pmod 7\)
\(12^6\equiv 1\pmod 7\Rightarrow 12^{2n}=12^{6k}\equiv 1\pmod 7\Rightarrow 12^{2n+1}\equiv 12\pmod 7\)
\(\Rightarrow 11^{n+2}+12^{2n+1}\equiv 14\equiv 0\pmod 7\) $(1)$
Lại có:
\(11^3\equiv 1\pmod {19}\Rightarrow 11^n=11^{3k}\equiv 1\pmod {19}\Rightarrow 11^{n+2}\equiv 7\pmod {19}\)
\(12^6\equiv 1\pmod {19}\Rightarrow 12^{2n}=12^{6k}\equiv 1\pmod {19}\Rightarrow 12^{2n+1}\equiv 12\pmod {19}\)
\(\Rightarrow 11^{n+2}+12^{2n+1}\equiv 19\equiv 0\pmod {19}\) $(2)$
Từ \((1),(2)\) kết hợp với \((7,19)=1\) suy ra \(11^{n+2}+12^{2n+1}\vdots (7.19=133)\) (đpcm)
11n+2+122n+1=121*11n+12*144n
=(133-12)*11n+12*144n=133*11n+(144n-11n)*12
ta có 133*11n\(⋮\)133,(144n-11n)*12\(⋮\)(144-11)
vậy 11n+2+122n+1\(⋮\)133(đpcm)

4a.
Số tự nhiên là A, ta có:
A = 7m + 5
A = 13n + 4
=>
A + 9 = 7m + 14 = 7(m + 2)
A + 9 = 13n + 13 = 13(n+1)
vậy A + 9 là bội số chung của 7 và 13
=> A + 9 = k.7.13 = 91k
<=> A = 91k - 9 = 91(k-1) + 82
vậy A chia cho 91 dư 82
4b.
Giả sử p là 1 số nguyên tố >3, do p không chia hết cho 3 nên p có dạng 3k + 1 hoặc 3k + 2
Vì p +4 là số nguyên tố nên p không thể có dạng 3k + 2
Vậy p có dạng 3k +1.
=> p + 8 = 3k + 9 chia hết cho 3 nên nó là hợp số.
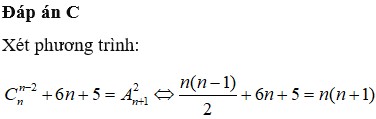
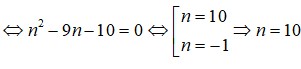
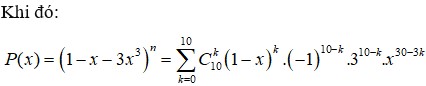
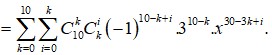




Câu hỏi của Đặng Trọng Hoàng - Chuyên mục hỏi đáp - Giúp tôi giải toán. - Học toán với OnlineMath