Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chứng minh:
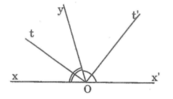
1) ∠tOy = 1/2. ∠xOy = 1/2. mo (Vì Ot là tia phân giác của góc xOy)
4) ∠x'Oy = 180o - ∠xOy = 180o - mo (Vì ∠x'Oy và ∠xOy kề bù)
2) ⇒ ∠t'Oy = 1/2. ∠x'Oy = 1/2. (180o - mo) (Vì Ot’ là phân giác của ∠x'Oy)
3) ⇒ ∠tOt' = ∠tOy + ∠t'Oy = 1/2. mo + 1/2. (180o - mo) = 90o.
Kết luận: Vậy hai tia phân giác của hai góc kề bù tạo thành góc vuông.

Vì Ot là tia phân giác của xOy => tOy = 1/2 . xOy
Vì Ot' là tia phân giác của yOx' => yOt' = 1/2 . yOx'
=> tOy + yOt' = 1/2 . xOy + 1/2 . yOx'
=> tOt' = 1/2 ( xOy + yOx' )
=> tOt' = 1/2 . 180độ ( kề bù )
=> tOt' = 90độ
=> Ot vuông góc với Ot' ( đpcm )

Bạn chép giải