Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Thay $x=-1$ vào phương trình $x^2-(3m+1)x+m-5=0$
$\Rightarrow (-1)^2-(3m+1).(-1)+m-5=0\\\Leftrightarrow 1+3m+1+m-5=0\\\Leftrightarrow 4m-3=0\\\Leftrightarrow 4m=3\\\Leftrightarrow m=\dfrac{3}{4}$
Vậy $m=\dfrac{3}{4}$
a, \(\Delta=m^2-4\left(-4\right)=m^2+16\)> 0
Vậy pt luôn có 2 nghiệm pb
b, Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=-4\end{matrix}\right.\)
Ta có \(\left(x_1+x_2\right)^2-2x_1x_2=5\)
Thay vào ta được \(m^2-2\left(-4\right)=5\Leftrightarrow m^2+3=0\left(voli\right)\)
Bạn ơi, mình có thể hỏi câu c được không ạ? Nếu không được thì không sao, mình cảm ơn câu trả lời của bạn ạ ^-^ chúc bạn một ngày tốt lành nhé.
Phương trình (1):
+ Vô nghiệm ⇔ Δ’ < 0 ⇔ 1 – 2m < 0 ⇔ 2m > 1 ⇔ m >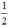 
+ Có nghiệm kép ⇔ Δ’ = 0 ⇔ 1 – 2m = 0 ⇔ m =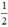 
+ Có hai nghiệm phân biệt ⇔ Δ’ > 0 ⇔ 1 – 2m > 0 ⇔ 2m < 1 ⇔ m <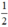 
Vậy: Phương trình (1) có hai nghiệm phân biệt khi m <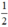 
; có nghiệm kép khi m = 
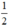và vô nghiệm khi m >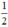 
\(x^2-mx+m-2=0\) (1) (a=1;b=-m;c=m-2)
\(\Delta=b^2-4ac=m^2-4.\left(-m\right).\left(m-2\right)\)
\(=m^2+4m^2-8m\)
=5m2-8m
Đến đây đưa về hằng đẳng thức mà ra dấu (-) bn xem đề có sai ko
\(\Delta=m^2-4>0\Rightarrow\left[{}\begin{matrix}m>2\\m< -2\end{matrix}\right.\)
Theo hệ thức Viet: \(x_1x_2=1\)
Mặt khác \(x_1\) là nghiệm pt nên:
\(x_1^2-mx_1+1=0\Rightarrow x_1^2+1=mx_1\)
Do đó:
\(x_2\left(x_1^2+1\right)=5\Leftrightarrow x_2.mx_1=5\)
\(\Leftrightarrow m.1=5\Rightarrow m=5\)
\(\text{Δ}=\left(-m\right)^2-4\left(-2m^2+3m-2\right)\)
\(=m^2+8m^2-12m+8\)
\(=9m^2-12m+8\)
\(=9m^2-12m+4+4=\left(3m-2\right)^2+4>0\)
Do đó: PHương trình luôn có hai nghiệm phân biệt
Phương trình có 2 nghiệm pb khi:
\(\Delta=m^2+4m^2>0\Leftrightarrow5m^2>0\)
\(\Rightarrow m\ne0\)
Δ=m2+4m2>0⇔5m2>0Δ=m2+4m2>0⇔5m2>0
m≠0