Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt S=x+y, P=x.y
Ta có:S=2a-1, x^2+y^2=S^2-2P=a^2+2a-3
\Rightarrow P=\frac{1}{2}[(2a-1)^2-(a^2+2a-3)]=\frac{1}{2}(3a^2-6a+4)
Trước hết tìm a để hệ có nghiệm.
Điều kiện để hệ có nghiệm:S^2-4P \geq 0 \Leftrightarrow (2a-1)^2-2(3a^2-6a+4)\geq 0
\Leftrightarrow -2a^2+8a-7 \geq 0 \leftrightarrow 2-\frac{\sqrt{2}}{2} \leq a \leq 2+\frac{\sqrt{2}}{2} (1)
Tìm a để P=\frac{1}{2}(3a^2-6a+4) đạt giá trị nhỏ nhất trên đoạn
[2-\frac{\sqrt{2}}{2} ;2+\frac{\sqrt{2}}{2}]
Ta có hoành độ đỉnh a_0=\frac{6}{2.3}=1Parabol có bề lõm quay lên do đó \min P=P(2-\frac{\sqrt{2}}{2} )$
Vậy với a=2-\frac{\sqrt{2}}{2} thì xy đạt giá trị nhỏ nhất.

ĐKXĐ: \(a\ne1;b\ne2;c\ne3\)
Đặt \(\frac{1}{a-1}=x;\frac{1}{b-2}=y;\frac{1}{c-3}=z\). Khi đó hệ phương trình đã cho tương đương:
\(\hept{\begin{cases}x+y+z=1\\x^2-2yz=-1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1-y-z\\\left(1-y-z\right)^2-2yz=-1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=1-y-z\\y^2+z^2+1+2yz-2y-2z-2yz=-1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=1-y-z\\y^2+z^2-2y-2z+2=0\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x=1-y-z\\\left(y-1\right)^2+\left(z-1\right)^2=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=-1\\y=1\\z=1\end{cases}}\).

c) Ta có: \(\left\{{}\begin{matrix}\dfrac{x+2}{x+1}+\dfrac{2}{y-2}=6\\\dfrac{5}{x+1}-\dfrac{1}{y-2}=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x+1}+\dfrac{2}{y-2}=5\\\dfrac{5}{x+1}-\dfrac{1}{y-2}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{x+1}+\dfrac{10}{y-2}=25\\\dfrac{5}{x+1}-\dfrac{1}{y-2}=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{11}{y-2}=22\\\dfrac{1}{x+1}+\dfrac{2}{y-2}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y-2=\dfrac{1}{2}\\\dfrac{1}{x+1}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+1=1\\y-2=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=\dfrac{5}{2}\end{matrix}\right.\)

1,
\(A=1+a+\frac{1}{b}+\frac{a}{b}+1+b+\frac{1}{a}+\frac{b}{a}\)
\(\ge1+1+2\sqrt{\frac{a}{b}.\frac{b}{a}}+a+b+\frac{a+b}{ab}=4+a+b+\frac{4\left(a+b\right)}{\left(a+b\right)^2}=4+a+b+\frac{4}{a+b}\)
lại có \(\left(1+1\right)\left(a^2+b^2\right)\ge\left(a+b\right)^2\Rightarrow a+b\le\sqrt{2}\)
\(4+a+b+\frac{4}{a+b}=4+\left(a+b+\frac{2}{a+b}\right)+\frac{2}{a+b}\ge4+2\sqrt{2}+\sqrt{2}=4+3\sqrt{2}\)
\(\Rightarrow A\ge4+3\sqrt{2}\)
câu 2
ta có:\(\left(2b^2+a^2\right)\left(2+1\right)\ge\left(2b+a\right)^2\Rightarrow3c\ge a+2b\)
\(\frac{1}{a}+\frac{2}{b}=\frac{1}{a}+\frac{4}{2b}\ge\frac{9}{a+2b}\ge\frac{9}{3c}=\frac{3}{c}\left(Q.E.D\right)\)

Ta có\(ab+bc+ca=\frac{\left(a+b+c\right)^2-\left(a^2+b^2+c^2\right)}{2}=1\)
Thay 1=ab+bc+ca vào, ta có
\(a\sqrt{\frac{\left(1+b^2\right)\left(1+c^2\right)}{1+a^2}}=a\sqrt{\frac{\left(a+b\right)\left(b+c\right)\left(a+c\right)\left(c+b\right)}{\left(a+b\right)\left(a+c\right)}}=a\left(b+c\right)\)
Tương tự rồi cộng lại, ta có
A=2(ab+bc+ca)=2
^_^

Áp dụng bđt Cô-si có'
\(\frac{1}{x}+\frac{1}{y}\ge\frac{2}{\sqrt{xy}}\ge\frac{2}{\frac{x+y}{2}}=\frac{4}{x+y}\)
\(\Rightarrow\frac{1}{x}+\frac{1}{y}\ge\frac{4}{x+y}\)
\(\Rightarrow\frac{1}{x+y}\le\frac{1}{4}\left(\frac{1}{x}+\frac{1}{y}\right)\)(1)
Áp dụng bđt trên ta được
\(\frac{1}{2a+b+c}=\frac{1}{\left(a+b\right)+\left(a+c\right)}\le\frac{1}{4}\left(\frac{1}{a+b}+\frac{1}{a+c}\right)\)
\(\Rightarrow\left(\frac{1}{2a+b+c}\right)^2\le\frac{1}{16}\left(\frac{1}{a+b}+\frac{1}{a+c}\right)^2\)
Chứng minh tương tự rồi cộng các vế lại cho nhau ta được
\(A\le\frac{1}{16}\left(\frac{1}{a+b}+\frac{1}{a+c}\right)^2+\frac{1}{16}\left(\frac{1}{a+c}+\frac{1}{b+c}\right)^2+\frac{1}{16}\left(\frac{1}{a+b}+\frac{1}{b+c}\right)^2\)
\(\Rightarrow16A\le\left(\frac{1}{a+b}+\frac{1}{a+c}\right)^2+\left(\frac{1}{a+c}+\frac{1}{b+c}\right)^2+\left(\frac{1}{a+b}+\frac{1}{b+c}\right)^2\)
\(=\frac{2}{\left(a+b\right)^2}+\frac{2}{\left(b+c\right)^2}+\frac{2}{\left(c+a\right)^2}+\frac{2}{\left(a+b\right)\left(a+c\right)}+\frac{2}{\left(b+c\right)\left(a+b\right)}+\frac{2}{\left(a+c\right)\left(b+c\right)}\)
Đặt \(\left(\frac{1}{a+b};\frac{1}{b+c};\frac{1}{c+a}\right)\rightarrow\left(x;y;z\right)\)
Khi đó \(16A\le2x^2+2y^2+2z^2+2xy+2yz+2zx\)
Ta có bđt phụ sau : \(xy+yz+zx\le x^2+y^2+z^2\)(tự chứng minh) (2)
Áp dụng ta được
\(16A\le4x^2+4y^2+4z^2=\frac{4}{\left(a+b\right)^2}+\frac{4}{\left(b+c\right)^2}+\frac{4}{\left(c+a\right)^2}\)
\(\Rightarrow4A\le\frac{1}{\left(a+b\right)^2}+\frac{1}{\left(b+c\right)^2}+\frac{1}{\left(c+a\right)^2}\)
Từ (1) \(\Rightarrow\frac{1}{\left(x+y\right)^2}\le\frac{1}{16}\left(\frac{1}{x}+\frac{1}{y}\right)^2\)(Bình phương 2 vế lên)
Áp dụng bđt này ta được
\(4A\le\frac{1}{16}\left(\frac{1}{a}+\frac{1}{b}\right)^2+\frac{1}{16}\left(\frac{1}{b}+\frac{1}{c}\right)^2+\frac{1}{16}\left(\frac{1}{c}+\frac{1}{a}\right)^2\)
\(\Rightarrow64A\le\frac{1}{a^2}+\frac{2}{ab}+\frac{1}{b^2}+\frac{1}{b^2}+\frac{2}{bc}+\frac{1}{c^2}+\frac{1}{c^2}+\frac{2}{ac}+\frac{1}{a^2}\)
\(\Rightarrow64A\le\frac{2}{a^2}+\frac{2}{b^2}+\frac{2}{c^2}+\frac{2}{ab}+\frac{2}{bc}+\frac{2}{ca}\)
\(\Rightarrow32A\le\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}+\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}\)
Áp dụng bđt (2) ta được \(\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}\le\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\)
\(\Rightarrow32A\le\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}+\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}=3+3=6\)
\(\Rightarrow A\le\frac{6}{32}=\frac{3}{16}\)
Dấu "=" xảy ra tại a=b=c = 1
#)Em thấy có link này có cách giải ngắn gọn hơn nek :
https://h.vn/hoi-dap/tim-kiem?q=cho+c%C3%A1c+s%E1%BB%91+th%E1%BB%B1c+d%C6%B0%C6%A1ng+a,b,c+thay+%C4%91%E1%BB%95i+lu%C3%B4n+th%E1%BB%8Fa+m%C3%A3n+1/a2+++1/b2+++1/c2+=3.T%C3%ACm+Max+P+=+1/(2a+b+c)2++1(2b+a+c)2++1/(2c+a+b)2&id=394201
Ai cần link này ib e nhé ! e gửi cho chị #Diệp Song Thiên đã ^^
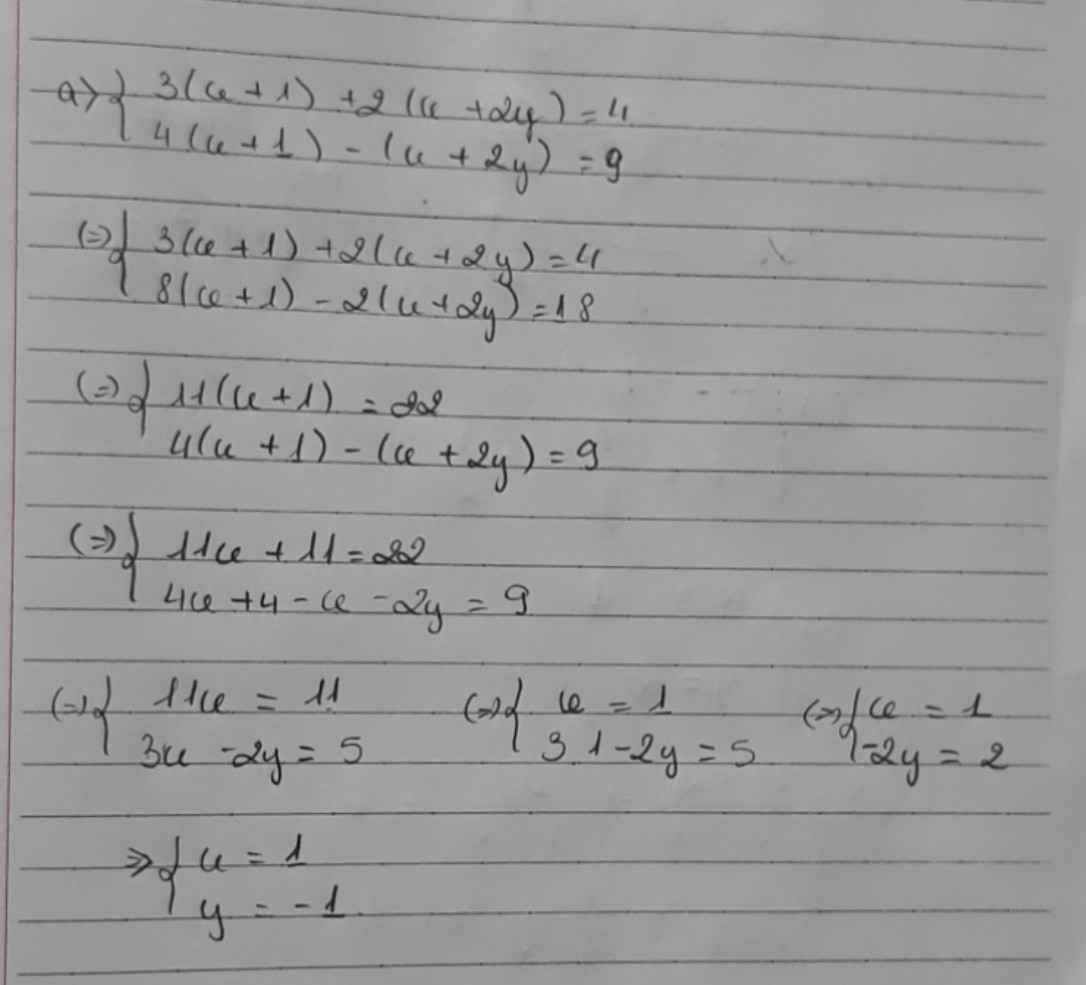
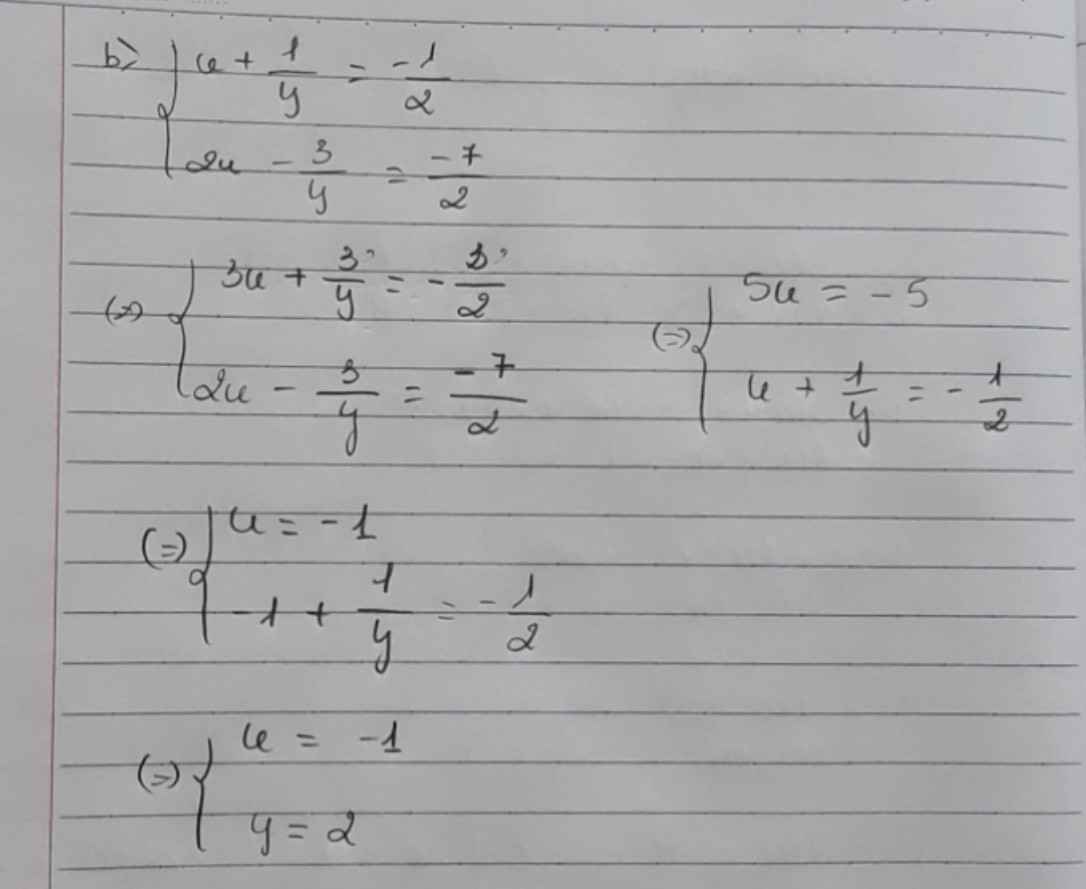
thief