Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. Đề thiếu
2. BĐT cần chứng minh tương đương:
\(a^4+b^4+c^4\ge abc\left(a+b+c\right)\)
Ta có:
\(a^4+b^4+c^4\ge\dfrac{1}{3}\left(a^2+b^2+c^2\right)^2\ge\dfrac{1}{3}\left(ab+bc+ca\right)^2\ge\dfrac{1}{3}.3abc\left(a+b+c\right)\) (đpcm)
3.
Ta có:
\(\left(a^6+b^6+1\right)\left(1+1+1\right)\ge\left(a^3+b^3+1\right)^2\)
\(\Rightarrow VT\ge\dfrac{1}{\sqrt{3}}\left(a^3+b^3+1+b^3+c^3+1+c^3+a^3+1\right)\)
\(VT\ge\sqrt{3}+\dfrac{2}{\sqrt{3}}\left(a^3+b^3+c^3\right)\)
Lại có:
\(a^3+b^3+1\ge3ab\) ; \(b^3+c^3+1\ge3bc\) ; \(c^3+a^3+1\ge3ca\)
\(\Rightarrow2\left(a^3+b^3+c^3\right)+3\ge3\left(ab+bc+ca\right)=9\)
\(\Rightarrow a^3+b^3+c^3\ge3\)
\(\Rightarrow VT\ge\sqrt{3}+\dfrac{6}{\sqrt{3}}=3\sqrt{3}\)
4.
Ta có:
\(a^3+1+1\ge3a\) ; \(b^3+1+1\ge3b\) ; \(c^3+1+1\ge3c\)
\(\Rightarrow a^3+b^3+c^3+6\ge3\left(a+b+c\right)=9\)
\(\Rightarrow a^3+b^3+c^3\ge3\)
5.
Ta có:
\(\dfrac{a}{b}+\dfrac{b}{c}\ge2\sqrt{\dfrac{a}{c}}\) ; \(\dfrac{a}{b}+\dfrac{c}{a}\ge2\sqrt{\dfrac{c}{b}}\) ; \(\dfrac{b}{c}+\dfrac{c}{a}\ge2\sqrt{\dfrac{b}{a}}\)
\(\Rightarrow\sqrt{\dfrac{b}{a}}+\sqrt{\dfrac{c}{b}}+\sqrt{\dfrac{a}{c}}\le\dfrac{a}{b}+\dfrac{b}{c}+\dfrac{c}{a}=1\)

Ta có:
\(x^4+y^4\ge\dfrac{1}{2}\left(x^2+y^2\right)^2=\dfrac{1}{2}\left(x^2+y^2\right)\left(x^2+y^2\right)\ge\dfrac{1}{2}.2xy\left(x^2+y^2\right)=xy\left(x^2+y^2\right)\)
Áp dụng:
\(P\le\dfrac{a}{a+bc\left(b^2+c^2\right)}+\dfrac{b}{b+ca\left(c^2+a^2\right)}+\dfrac{c}{c+ab\left(a^2+b^2\right)}\)
\(P\le\dfrac{a^2}{a^2+abc\left(b^2+c^2\right)}+\dfrac{b^2}{b^2+abc\left(c^2+a^2\right)}+\dfrac{c^2}{c^2+abc\left(a^2+b^2\right)}=1\)
Dấu "=" xảy ra khi \(a=b=c=1\)

\(\dfrac{a}{a+2\sqrt{\left(a+bc\right)}}=\dfrac{a}{a+2\sqrt{a\left(a+b+c\right)+bc}}=\dfrac{a}{a+2\sqrt{\left(a+b\right)\left(a+c\right)}}\)
\(=\dfrac{a}{a+\dfrac{\sqrt{\left(a+b\right)\left(a+c\right)}}{2}+\dfrac{\sqrt{\left(a+b\right)\left(a+c\right)}}{2}+\dfrac{\sqrt{\left(a+b\right)\left(a+c\right)}}{2}+\dfrac{\sqrt{\left(a+b\right)\left(a+c\right)}}{2}}\)
\(\le\dfrac{a}{5^2}\left(\dfrac{1}{a}+\dfrac{1}{\dfrac{\sqrt{\left(a+b\right)\left(a+c\right)}}{2}}+\dfrac{1}{\dfrac{\sqrt{\left(a+b\right)\left(a+c\right)}}{2}}+\dfrac{1}{\dfrac{\sqrt{\left(a+b\right)\left(a+c\right)}}{2}}+\dfrac{1}{\dfrac{\sqrt{\left(a+b\right)\left(a+c\right)}}{2}}\right)\)
\(=\dfrac{a}{25}\left(\dfrac{1}{a}+\dfrac{8}{\sqrt{\left(a+b\right)\left(a+c\right)}}\right)=\dfrac{1}{25}+\dfrac{8}{25}.\dfrac{a}{\sqrt{\left(a+b\right)\left(a+c\right)}}\)
\(\le\dfrac{1}{25}+\dfrac{4}{25}\left(\dfrac{a}{a+b}+\dfrac{a}{a+c}\right)\)
Tương tự:
\(\dfrac{b}{b+2\sqrt{b+ac}}\le\dfrac{1}{25}+\dfrac{4}{25}\left(\dfrac{b}{a+b}+\dfrac{b}{b+c}\right)\)
\(\dfrac{c}{c+2\sqrt{c+ab}}\le\dfrac{1}{25}+\dfrac{4}{25}\left(\dfrac{c}{a+c}+\dfrac{c}{b+c}\right)\)
Cộng vế:
\(P\le\dfrac{3}{25}+\dfrac{4}{25}\left(\dfrac{a+b}{a+b}+\dfrac{b+c}{b+c}+\dfrac{c+a}{c+a}\right)=\dfrac{15}{25}=\dfrac{3}{5}\)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{3}\)

a: vecto AB=(-3;-4)
vecto AC=(3;-2)
Vì -3/3<>-4/2-2
nên A,B,C là ba đỉnh của 1 tam giác
b: Tọa độ G là:
x=(2-1+5)/3=2 và y=(3-1+1)/3=2
=>G(2;2) và A(2;3)
Tọa độ I là:
x=(2+2)/2=2 và y=(2+3)/2=2,5
c: K thuộc Oy nên K(0;y)
vecto AI=(0;-0,5); vecto AK=(-2;y-3)
Theo đề, ta có:
0/-2=-0,5/y-3
=>-0,5/y-3=0
=>Ko có K thỏa mãn


\(\dfrac{ab}{a+3b+2c}=\dfrac{ab}{\left(a+c\right)+\left(b+c\right)+2b}\le\dfrac{1}{9}\left(\dfrac{ab}{a+c}+\dfrac{ab}{b+c}+\dfrac{ab}{2b}\right)\)
\(=\dfrac{1}{9}\left(\dfrac{ab}{a+c}+\dfrac{ab}{b+c}+\dfrac{a}{2}\right)\)
Tương tự:
\(\dfrac{bc}{b+3c+2a}\le\dfrac{1}{9}\left(\dfrac{bc}{a+b}+\dfrac{bc}{a+c}+\dfrac{b}{2}\right)\)
\(\dfrac{ac}{c+3a+2b}\le\dfrac{1}{9}\left(\dfrac{ac}{b+c}+\dfrac{ac}{a+b}+\dfrac{c}{2}\right)\)
Cộng vế:
\(P\le\dfrac{1}{9}\left(\dfrac{bc+ac}{a+b}+\dfrac{bc+ab}{a+c}+\dfrac{ab+ac}{b+c}+\dfrac{a+b+c}{2}\right)\)
\(P\le\dfrac{1}{9}.\left(a+b+c+\dfrac{a+b+c}{2}\right)=\dfrac{1}{2}\)
Dấu "=" xảy ra khi \(a=b=c=1\)

Để ý rằng \(a+b+c=1\) hay \(\left(a+b+c\right)^2=1\)nên ta cần biển đổi a,b,c xuất hiện các đại lượng \(\frac{\sqrt{a}}{\sqrt{c+2b}};\frac{\sqrt{b}}{\sqrt{a+2c}};\frac{\sqrt{c}}{\sqrt{b+2a}}\)nên ta biển đổi như sau:
\(a+b+c=\frac{\sqrt{a}}{\sqrt{c+2b}}\sqrt{a\left(c+2b\right)}+\frac{\sqrt{b}}{\sqrt{a+2c}}\sqrt{b\left(a+2c\right)}+\frac{\sqrt{c}}{\sqrt{b+2a}}\sqrt{c\left(b+2a\right)}\)
Khi đó ta được:
\(\left(a+b+c\right)^2=\left[\frac{\sqrt{a}}{\sqrt{c+2b}}\sqrt{a\left(c+2b\right)}+\frac{\sqrt{b}}{\sqrt{a+2c}}\sqrt{b\left(a+2c\right)}+\frac{\sqrt{c}}{\sqrt{b+2a}}\sqrt{c\left(b+2a\right)}\right]^2\)
Theo bất đẳng thức Bunhiacopxiki ta được:
\(\left[\frac{\sqrt{a}}{\sqrt{c+2b}}\sqrt{a\left(c+2b\right)}+\frac{\sqrt{b}}{\sqrt{a+2c}}\sqrt{b\left(a+2c\right)}+\frac{\sqrt{c}}{\sqrt{b+2a}}\sqrt{c\left(b+2a\right)}\right]\)
\(\le\left(\frac{a}{c+2b}+\frac{b}{a+2c}+\frac{c}{b+2a}\right)\left[a\left(c+2b\right)b\left(a+2c\right)c\left(b+2a\right)\right]\)
Như vậy lúc này ta được:
\(\frac{a}{c+2b}+\frac{b}{a+2c}+\frac{c}{b+2a}\ge\frac{\left(a+b+c\right)^2}{3\left(ab+bc+ca\right)}\)
Vậy bài toán đã được chứng minh.

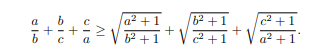
\(\dfrac{a-1}{a}+\dfrac{b-1}{b}+\dfrac{c-1}{c}+6=9-\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\le9-\dfrac{9}{a+b+c}=9-9=0\left(đpcm\right)\)
cảm ơn ạ